初中数学相似多边形的性质选择题

如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连接DF，分析下列五个结论：①△AEF∽△CAB；②CF=2AF；③DF=DC；④tan∠CAD=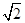；⑤S_{四边形CDEF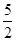}=S_△ABF，其中正确的结论有（ ）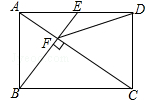

A．5个

B．4个

C．3个

D．2个

．如图，已知AB∥CD，AD与BC相交于点O，AO：DO=1：2，那么下列式子正）确的是（ 

A．BO：BC=1：2

B．CD：AB=2：1

C．CO：BC=1：2

D．AD：DO=3：1

如图，l₁∥l₂∥l₃，直线a，b与l₁、l₂、l₃分别相交于A、B、C和点D、E、F．若，DE=4，则EF的长是（ ）

A．      B．      C．6      D．10

如图，矩形OABC的顶点O是坐标原点，边OA在x轴上，边OC在y轴上．若矩形OA₁B₁C₁与矩形OABC关于点O位似，且矩形OA₁B₁C₁的面积等于矩形OABC面积的，则点B₁的坐标是（ ）

A．（3，2）

B．（-2，-3）

C．（2，3）或（-2，-3）

D．（3，2）或（-3，-2）

如图，数学兴趣小组的小颖想测量教学楼前的一棵树的树高，下午课外活动时她测得一根长为1m的竹竿的影长是0．8m，但当她马上测量树高时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上（如图），他先测得留在墙壁上的影高为1．2m，又测得地面的影长为2．6m，请你帮她算一下，树高是（ ）

A．3．25m

B．4．25m

C．4．45m

D．4．75m

如图，在△ABC，P为AB上一点，连结CP，下列条件中不能判定△ACP∽△ABC的是（   ）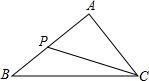

A．∠ACP=∠B	B．∠APC=∠ACB
C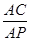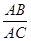．＝	D．=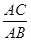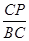

如图，在△ABC中，AD平分∠BAC,按如下步骤作图：第一步，分别以点A、D为圆心，以大于的长为半径在AD的两侧作弧，交于两点M、N;第二步，连结MN，分别交AB、AC于点E、F；第三步，连结DE、DF．．若BD=6，AF=4，CD=3，则BE的长是（    ）

A．2    B．4    C．6  D．8

下列命题中的真命题是（ ）

A．两边和一角分别相等的两个三角形全等

B．相似三角形的面积比等于相似比

C．正方形不是中心对称图形

D．圆内接四边形的对角互补

如图，△ABE和△CDE是以点E为位似中心的位似图形，已知点A（3，4），点C（2，2），点D（3，1），则点D的对应点B的坐标是（     ）．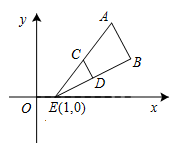

A．（4，2）

B．（4，1）

C．（5，2）

D．（5，1）

一块含30°角的直角三角板（如图），它的斜边AB=8cm，里面空心△DEF的各边与△ABC的对应边平行，且各对应边的距离都是1cm，那么△DEF的周长是（  ）

A．5cm

B．6cm

C．（6−）cm

D．（3+）cm

如图，△ABC中，CD⊥AB于D，E是AC的中点，∠B=45°，若AD=6，DE=5，则BC的长等于        ．

如图1，点E为矩形ABCD边AD上一点，点P，点Q同时从点B出发，点P沿BE→ED→DC运动到点C停止，点Q沿BC运动到点C停止，它们的运动速度都是1cm/s．设P，Q出发t秒时，△BPQ的面积为ycm²，已知y与t的函数关系的图象如图2（曲线OM为抛物线的一部分）．则下列结论：

①AD=BE=5cm；  
②当0＜t≤5时，；
③直线NH的解析式为；
④若△ABE与△QBP相似，则秒．
其中正确结论的个数为（   ）    

A．4

B．3

C．2

D．1

如图，下列条件不能判定△ADB∽△ABC的是（ ）

A．∠ABD=∠ACB	B．∠ADB=∠ABC
C．AB^2=AD•AC	D．=

如图，以点O为位似中心，将△ABC放大得到△DEF．若AD=OA，则△ABC与△DEF的面积之比为（ ）．

A．1：2

B．1：4

C．1：5

D．1：6

如图，已知D，E分别是△ABC的AB，AC边上的点，DE∥BC，且BD=3AD．那么AE：AC等于（   ）

A．2 ： 3         B．1 ： 2      C．1 ： 3           D．1 ：4