如图,在正方形ABCD中,E是AD的中点,F是AB边上一点,BF=3AF,则下列四个结论:
①△AEF∽△DCE;
②CE平分∠DCF;
③点B、C、E、F四个点在同一个圆上;
④直线EF是△DCE的外接圆的切线;
其中,正确的个数是( )
A.1个 B.2个 C. 3个 D. 4个
如图,正方形ABCD和正方形OEFG中,点A和点F的坐标分别为 (3,2),(-1,-1),则两个正方形的位似中心的坐标是( )
| A.(1,0) |
| B.(-5,-1) |
| C.(1,0)或(-5,-1) |
| D.(1,0)或(-5,-2) |
如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③ =
= ;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
A.①② B.①②③ C.①④ D.①②④
高4米的旗杆在水平地面上的影长5米,此时测得附近一个建筑物的影子长20米,则该建筑物的高是 ( )
| A.16米 | B.20米 | C.24米 | D.30米 |
手工制作课上,小红利用一些花布的边角料,剪裁后装裱手工画.下面四个图案是她剪裁出的
空心不等边三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相同,那么,每个图
案中花边的内外边缘所围成的几何图形不相似的是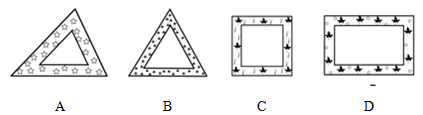
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△DEF:S△BCF =( )
| A.4:9 | B.1:4 | C.1:2 | D.1:1 |
如图, 中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则☉C的半径为( )
中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则☉C的半径为( )
| A.2.3 | B.2.4 | C.2.5 | D.2.6 |
如图,小明同学用自制的直角三角形纸板EFG测量树的高度AB,他调整自己的位置,设法使斜边EG保持水平,并且边EF所在的直线经过点A.已知纸板的两条直角边EF=60cm,FG=30cm,测得小刚与树的水平距离BD=8m,边EG离地面的高度DE=1.6m,则树的高度AB等于( )
A.5m B.5.5m C.5.6m D.5.8m
如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则端点C的坐标为( ).
后得到线段CD,则端点C的坐标为( ).
| A.(3,3) | B.(4,3) | C.(3,1) | D.(4,1) |
如图,直线y=x+1分别与x轴、y轴相交于点A、B,以点A为圆心,AB长为半径画弧交x轴于点A1,再过点A1作x轴的垂线交直线于点 B1,以点A为圆心,AB1长为半径画弧交x轴于点A2,……,
按此做法进行下去,则点A8的坐标是
A.(15,0) B.(16,0) C.(8 ,0) D.(
,0) D.( ,0)
,0)
如图,AD∥BE∥CF,直线l1、l2这与三条平行线分别交于点A、B、C和点D、E、F.已知AB=l,BC=3,DE =2,则EF'的长为( )
A.4 B.5 C.6 D.8
如图, ∥
∥ ∥
∥ ,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知
,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知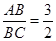 ,则
,则 的值为( )
的值为( )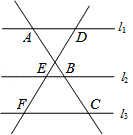
A. B.
B. C.
C. D.
D.
如图,在Rt△ABC中,∠ABC=90°,AB=BC.点D是线段AB上的一点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:
① ;
;
②若点D是AB的中点,则AF= AB;
AB;
③当B、C、F、D四点在同一个圆上时,DF=DB;
④若 ,则
,则 .
.
其中正确的结论序号是( )
A.①② B.③④ C.①②③ D.①②③④
试题篮
()