如图,△ABC∽△ADE,∠ADE=∠B,则下列比例式正确的是( )
A. |
B. |
C. |
D. |
在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图①的方式向外扩张,得到新三角形,它们的对应边间距均为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图②的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )
| A.两人都对 | B.两人都不对 |
| C.甲对,乙不对 | D.甲不对,乙对 |
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B,C两点的坐标分别是( )
A.( ,3),( ,3),( ,4) ,4) |
B.( ,3),( ,3),( ,4) ,4) |
C. ,( ,( ,4) ,4) |
D. ,( ,( ,4) ,4) |
如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF︰FC等于( )
| A.3︰2 | B.3︰1 | C.1︰1 | D.1︰2 |
在△ABC和△A1B1C1中,有下列四个命题:
(1)若AB=A1B1,AC=A1C1,∠A=∠A1,则△ABC≌△A1B1C1;
(2)若AB=A1B1,AC=A1C1,∠B=∠B1,则△ABC≌△A1B1C1;
(3)若∠A=∠A1,∠C=∠C1,则△ABC∽△A1B1C1;
(4)若AC︰A1C1=CB︰C1B1,∠C=∠C1,则△ABC∽△A1B1C1.
其中真命题的个数为( )
| A.4 | B.3 | C.2 | D.1 |
如图,在△ABC中,AE交BC于点D,∠C=∠E,AD︰DE=3︰5,AE=8,BD=4,则DC的长等于( )
A. |
B. |
C. |
D. |
如图所示,在△ABC中,DE∥BC,DE分别与AB,AC相交于点D,E.若AD=4,DB=2,则DE︰BC的值为( )
A. |
B. |
C. |
D. |
若△ABC∽△DEF,AB=5,BC=3,DF=7,EF=9,则△ABC与△DEF的相似比是( )
A. |
B. |
C. |
D. |
如图,D、E分别是△ABC的边AB、BC上的点,且DE//AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
A. B.
B.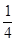 C.
C.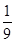 D.
D.
如图,线段CD两个端点的坐标分别为C(1,2),D(2,0),以原点为位似中心,将线段CD
放大得到线段AB,若点B的坐标为(5,0),则点A的坐标为( )
| A.(2,5) | B.(2.5,5) | C.(3,5) | D.(3,6) |
如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为10m,则A,B间的距离为( ).
| A.15m | B.25m | C.30m | D.20m |
已知:如图,在等边三角形ABC中,M、N分别是AB、AC的中点,D是MN上任意一点,CD、BD的延长线分别与AB、AC交于F、E,若 ,则等边三角形ABC的边长为( )
,则等边三角形ABC的边长为( )
A. B.
B. C.
C. D.1
D.1
如图,已知Rt△ABC中,∠BAC=90°,AD⊥BC,BD=9,CD=16,下列选项结论中,此题数据不能验证的结论选项是( ).
A. |
B. |
C. |
D. |
试题篮
()