夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )
| A.8m | B.6.4m | C.4.8m | D.10m |
已知△ABC∽△DEF,若△ABC与△DEF的相似比为3∶4,则△ABC与△DEF的面积比为( )
| A.4∶3 | B.3∶4 | C.16∶9 | D.9∶16 |
如图,已知BO是△ABC的外接圆的半径,CD⊥AB于D.若AD=3,BD=8,CD=6,则BO的长为 ( )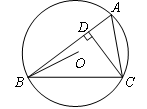
A.6 B.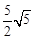 C.
C.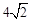 D.
D.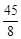
已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积比为( )
| A.4:3 | B.3:4 | C.16:9 | D.9:16 |
小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
| A.10米 | B.12米 | C.15米 | D.22.5米 |
如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有( )
A.1条 B.2条 C.3条 D.4条
如图,每个正方形网格的边长为1个单位长度,将△ABC的三边分别扩大一倍得到△ (顶点均在格点上),若它们是以点P为位似中心的位似图形,则点P的坐标是( )
(顶点均在格点上),若它们是以点P为位似中心的位似图形,则点P的坐标是( )
A. |
B. |
C. |
D. |
如图,在△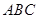 中,点D、E分别在边AB 、AC上,下列比例式不能判定
中,点D、E分别在边AB 、AC上,下列比例式不能判定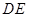 ∥
∥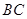 的是( ).
的是( ).
A.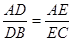 ; B.
; B.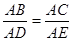 ;C.
;C.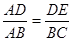 ;D.
;D.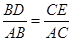 .
.
如图,点 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 都是
都是 方格纸(每个小方格均为正方形)中的格点,为使△
方格纸(每个小方格均为正方形)中的格点,为使△ ∽△
∽△ ,则点
,则点 应是
应是 、
、 、
、 、
、 四点中的( ).
四点中的( ).
A. ; ; |
B. ; ; |
C. ; ; |
D. . . |
在比例尺为 的地图上测得
的地图上测得 、
、 两地间的图上距离为
两地间的图上距离为 ,则
,则 两地间的实际距离为( ).
两地间的实际距离为( ).
A. ; ; |
B. ; ; |
C. ; ; |
D. . . |
下列四组数中,能组成比例的是( ).
A. , , , , , , ; ; |
B. , , , , , , ; ; |
C. , , , , , , ; ; |
D. , , , , , , . . |
如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接BD、DE.若BD平分∠ABC,则下列结论不一定成立的是( )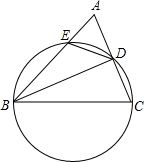
A.BD⊥AC B.AC2=2AB·AE
C.BC=2AD D.△ADE是等腰三角形
如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.
其中正确的结论有
| A.5个 | B.4个 | C.3个 | D.2个 |
试题篮
()