初中数学相似多边形的性质选择题

已知△ABC∽△DEF，若△ABC与△DEF的相似比为3：4，则△ABC与△DEF的面积之比为【   】

A．4：3

B．3：4

C．16：9

D．9：16

如图，在平行四边形ABCD中，点E在AD上，连接CE并延长与BA的延长线交于点F，若AE=2ED，CD=3cm，则AF的长为【   】

A．5cm

B．6cm

C．7cm

D．8cm

如图，DE是△ABC的中位线，延长DE至F使EF=DE，连接CF，则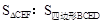的值为【   】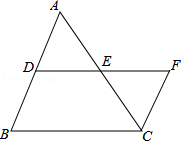

A．1：3

B．2：3

C．1：4

D．2：5

如图，在▱ABCD中，E是AD边上的中点，连接BE，并延长BE交CD延长线于点F，则△EDF与△BCF的周长之比是【   】

A．1：2

B．1：3

C．1：4

D．1：5

下列命题中，真命题是【   】

A．位似图形一定是相似图形	B．等腰梯形既是轴对称图形又是中心对称图形
C．四条边相等的四边形是正方形	D．垂直于同一直线的两条直线互相垂直

如图，在圆O上有定点C和动点P，位于直径AB的异侧，过点C作CP的垂线，与PB的延长线交于点Q，已知：圆O半径为，tan∠ABC＝，则CQ的最大值是

A．5

B．

C．

D．

如图．在ABCD中，AB＝6、AD＝9，∠BAD的平分线交BC于点E，DC的延长线于点F, BG⊥AE，垂足为G，若BG＝4，则△CEF的面积是

A．2

B．

C．3

D．4

如图，M是Rt△ABC的斜边BC上异于B、C的一定点，过M点作直线截△ABC，使截得的三角形与△ABC相似，这样的直线共有

A．1条       B．2条      C．3条      D．4条

直线l₁∥l₂∥l₃，且l₁与l₂的距离为1，l₂与l₃的距离为3，把一块含有45°角的直角三角形如图放置，顶点A，B，C恰好分别落在三条直线上，AC与直线l₂交于点D，则线段BD的长度为

A．

B．

C．

D．

如图，Rt△ABC中，∠A=90°，AD⊥BC于点D，若BD：CD=3：2，则tanB=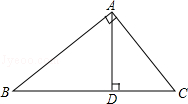

A．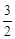

B．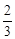

C．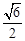

D．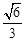

如图，在△ABC中，BC＞AC，点D在BC上，且DC=AC，∠ACB的平分线CE交AD于E，点F是AB的中点，则S_△AEF：S_{四边形BDEF}为

A．3：4

B．1：2

C．2：3

D．1：3

如图，在平行四边形ABCD中，AB=6，AD=9，∠BAD的平分线交BC于E，交DC的延长线于F，BG⊥AE于G，BG=，则△EFC的周长为【   】

A．11

B．10

C．9

D．8

（2013年四川南充3分） 如图1，点E为矩形ABCD边AD上一点，点P，点Q同时从点B出发，点P沿BE→ED→DC 运动到点C停止，点Q沿BC运动到点C停止，它们运动的速度都是1cm/s，设P，Q出发t秒时，△BPQ的面积为ycm，已知y与t的函数关系的图形如图2（曲线OM为抛物线的一部分），则下列结论：①AD=BE=5cm；②当0＜t≤5时，；③直线NH的解析式为；④若△ABE与△QBP相似，则t=秒。其中正确的结论个数为【   】

A．4

B．3

C．2

D．1

如图，∠BAC=∠DAF=90°，AB=AC，AD=AF，点D、E为BC边上的两点，且∠DAE=45°，连接EF、BF，则下列结论：①△AED≌△AEF；②△ABE∽△ACD；③BE+DC＞DE；④BE²+DC²=DE²，
其中正确的有【   】个．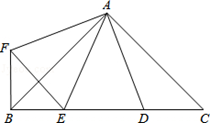

A．1     B．2      C．3     D．4

如图，在等腰直角△ACB=90°，O是斜边AB的中点，点D、E分别在直角边AC、BC上，且∠DOE=90°，DE交OC于点P．则下列结论：
（1）图形中全等的三角形只有两对；（2）△ABC的面积等于四边形CDOE的面积的2倍；（3）CD+CE=OA；（4）AD²+BE²=2OP•OC．其中正确的结论有【　　】

A．1个　　　　　B．2个　　　　　C．3个　　　　　D．4个