如图,正方形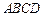 中,点F在边BC上,E在边BA的延长线上,
中,点F在边BC上,E在边BA的延长线上,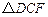 按顺时针方向旋转后能与
按顺时针方向旋转后能与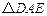 重合.
重合.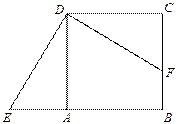
(1)旋转中心是点 ;最少旋转了 度;
(2)若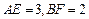 ,求四边形
,求四边形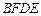 的面积.
的面积.
(1) 如图一,等边三角形MNP的边长为1,线段AB的长为4,点M与A重合,点N在线段AB上. △MNP沿线段AB按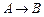 的方向滚动, 直至△MNP中有一个点与点B重合为止,则点P经过的路程为 ;
的方向滚动, 直至△MNP中有一个点与点B重合为止,则点P经过的路程为 ;
(2)如图二,正方形MNPQ的边长为1,正方形ABCD的边长为2,点M与点A重合,点N在线段AB上, 点P在正方形内部,正方形MNPQ沿正方形ABCD的边按 的方向滚动,始终保持M,N,P,Q四点在正方形内部或边界上,直至正方形MNPQ回到初始位置为止,则点P经过的最短路程为 .
的方向滚动,始终保持M,N,P,Q四点在正方形内部或边界上,直至正方形MNPQ回到初始位置为止,则点P经过的最短路程为 .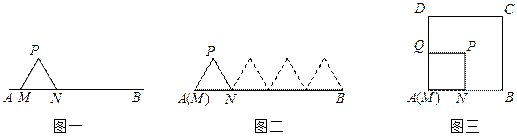
(注:以△MNP为例,△MNP沿线段AB按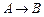 的方向滚动指的是先以顶点N为中心顺时针旋转,当顶点P落在线段AB上时, 再以顶点P为中心顺时针旋转,如此继续. 多边形沿直线滚动与此类似.)
的方向滚动指的是先以顶点N为中心顺时针旋转,当顶点P落在线段AB上时, 再以顶点P为中心顺时针旋转,如此继续. 多边形沿直线滚动与此类似.)
如图,E,B,A,F四点共线,点D是正三角形ABC的边AC的中点,点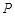 是直线
是直线 上异于A,B的一个动点,且满足
上异于A,B的一个动点,且满足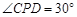 ,则 ( )
,则 ( )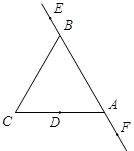
A.点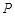 一定在射线 一定在射线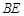 上 上 |
B.点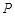 一定在线段 一定在线段 上 上 |
C.点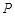 可以在射线 可以在射线 上,也可以在线段 上,也可以在线段 上 上 |
D.点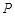 可以在射线 可以在射线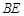 上,也可以在线段 上,也可以在线段 上 上 |
△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,把一个三角板的直角顶点放在点D处,将三角板绕点D旋转且使两条直角边分别交AB、AC于E、F .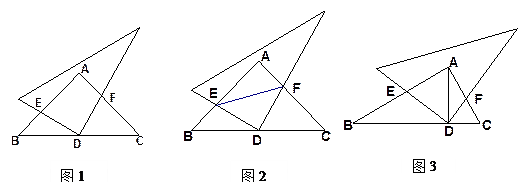
(1)如图1,观察旋转过程,猜想线段AF与BE的数量关系并证明你的结论;
(2)如图2,若连接EF,试探索线段BE、EF、FC之间的数量关系,直接写出你的结论(不需证明);
(3)如图3,若将“AB=AC,点D是BC的中点”改为:“∠B=30°,AD⊥BC于点D”,其余条件不变,探索(1)中结论是否成立?若不成立,请探索关于AF、BE的比值.
两个长为2,宽为1的矩形ABCD和矩形EFGH如图1所示摆放在直线l上,DE=2,将矩形ABCD绕点D顺时针旋转 角(
角( ) ,将矩形EFGH绕点E逆时针旋转相同的角度.
) ,将矩形EFGH绕点E逆时针旋转相同的角度.
(1)当两个矩形旋转到顶点C,F重合时(如图2),∠DCE=" " °,点C到直线l的距离等于 , =" " °;(2)利用图3思考:在旋转的过程中,矩形ABCD和矩形EFGH重合部分为正方形时,
=" " °;(2)利用图3思考:在旋转的过程中,矩形ABCD和矩形EFGH重合部分为正方形时, =" " °.
=" " °.
如图,在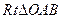 中,
中,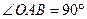 ,
,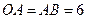 ,将
,将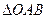 绕点
绕点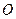 沿逆时针方向旋转
沿逆时针方向旋转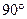 得到
得到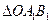 .
.
(1)线段 的长是 ,
的长是 ,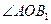 的度数是 ;
的度数是 ;
(2)连结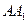 ,求证:四边形
,求证:四边形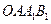 是平行四边形;
是平行四边形;
将一副三角板按如图1位置摆放,使得两块三角板的直角边AC和MD重合.已知AB="AC=8" cm,将△MED绕点A(M)逆时针旋转60°后(图2),两个三角形重叠(阴影)部分的面积是 ▲ cm2
如图,已知A(1,-3),B(-2,-2),C(2,0),
(1)将△ABC向右平移,使B点落在y轴上,画出平移后的△A1B1C1
(2)画出△A1B1C1关于直线y=1对称的△A2B2C2
(3)求S△ABC
如图9,在正方形网格中每个小正方形的边长都是单位1,已知△ABC和△A1B1C1关于点O成中心对称,点O直线x上.
(1)在图中标出对称中心O的位置;
(2)画出△A1B1C1关于直线x对称的△A2B2C2;
(3)△ABC与△A2B2C2满足什么几何变换?
如图2,点A、D、B、E在同一直线上,△ABC≌△DEF,AB=6,AE=10,则DB等于
A.2 B.2.5 C.3 D.4
试题篮
()