初中数学一元二次方程的最值选择题

已知x₁，x₂是方程x²－x－3＝0的两个根，那么x₁＋x₂的值是（   ）

A．1

B．5

C．7

D．

关于的方程有两个不相等的实数根，则的取值范围是（   ）

A．k＞－1

B．k≥－1

C．k＜－1

D．k≤－1

用配方法解方程x²-2x-1＝0时，配方后所得的方程为 （   ）

A．（x＋1）^2＝0	B．（x-1）^2＝0
C．（x＋1）^2＝2	D．（x-1）^2＝2

x₁，x₂是关于x的一元二次方程x²﹣mx+m﹣2=0的两个实数根，是否存在实数m使成立？则正确的结论是（ ）

A．m=0时成立

B．m=2时成立

C．m=0或2时成立

D．不存在

若实数、满足，则的值为（    ）

A．－2

B．4

C．4或－2

D．－4或2

若x=3是方程x²﹣5x+m=0的一个根，则这个方程的另一个根是（ ）

A．﹣2

B．2

C．﹣5

D．5

用10米长的铝材制成一个矩形窗框，使它的面积为6平方米．若设它的一条边长为x米，则根据题意可列出关于x的方程为（ ）

A．x（5+x）= 6	B．x（5 – x ）= 6
C．x（10 – x ）= 6	D．x（10 - 2x ）= 6

关于的一元二次方程有两个不相等实数根，则的取值范围是（     ）       

A．

B．

C．

D．

若关于x的一元二次方程的两个根为x₁=1，x₂=2，则这个方程是（ ）

A．x^2+3x-2=0

B．x^2-3x+2=0

C．x^2-2x+3=0

D．x^2+3x+2=0

根据下列表格的对应值：请判断方程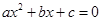 （a≠0，a，b，c为常数）一个解x的范围是（  ）．

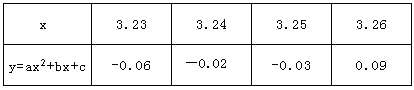
A．3＜x＜3．23	B．3．23＜x＜3．24
C．3．24＜x＜3．25	D．3．25＜x＜3．26

根据关于x的一元二次方程，可列表如下：

x	0	0．5	1	1．1	1．2	1．3
	－15	－8．75	－2	－0．59	0．84	2．29

 
则方程的正数解满足（    ）
A．0．5＜＜1        B．1＜＜1．1    
C．1．1＜＜1．2     D．1．2＜＜1．3

关于x的一元二次方程有一个根为0，则a的值是（   ）

A．±1

B．-1

C．1

D．0

小红按某种规律写出4个方程：①；②；③；④．按此规律，第五个方程的两个根为（    ）

A．-2、3

B．2、-3

C．-2、-3

D．2、3

下列命题中，真命题是（    ）

A．两组数据1、2、3、4、5与21、22、23、24、25的离散程度相同

B．若点C是线段AB的黄金分割点，且AB=10，则AC≈6．18

C．等腰三角形的边长是方程的两个解，则这个三角形的底边长为2或4

D．在平行光线的照射下，不同物体的物高与影长成比例

设a和b是方程x2+x-2009的两个实数根，则的值为（     ）

A．2006

B．2007

C．2008

D．2009