如图 ,已知抛物线过点A(0,6),B(2,0),C(7,
,已知抛物线过点A(0,6),B(2,0),C(7, ).
).
(1)求抛物线的解析式;
(2)若D是抛物线的顶点,E是抛物线的对称轴与直线AC的交点,F与E关于D对称,求证:∠CFE=∠AFE;
(3)在y轴上是否存在这样的点P,使△AFP与△FDC相似,若有请求出所有和条件的点P的坐标,若没有,请说明理由.
如图,已知抛物线y=﹣x2+bx+9﹣b2(b为常数)经过坐标原点O,且与x轴交于另一点E.其顶点M在第一象限.
(1)求该抛物线所对应的函数关系式;
(2)设点A是该抛物线上位于x轴上方,且在其对称轴左侧的一个动点;过点A作x轴的平行线交该抛物线于另一点D,再作AB⊥x轴于点B.DE⊥x轴于点C.
①当线段AB、BC的长都是整数个单位长度时,求矩形ABCD的周长;
②求矩形ABCD的周长的最大值,并写出此时点A的坐标;
③当矩形ABCD的周长取得最大值时,它的面积是否也同时取得最大值?请判断井说明理由.
(11·曲靖)一名男生推铅球,铅球行进高度y(单位:m)与水平距离x

(1)求铅球推出的水平距离;
(2)通过计算说明铅球行进高度能否达到4m。
(11·兵团维吾尔)已知抛物线y=-x2+4x-3与x轴交于A、B两点(A
点在B点左侧),顶点为P.
(1)求A、B、P三点的坐标;
(2)在 直角坐标系中,用列表描点法作出抛物线的图象,并根据图象写出x取何值时,函
直角坐标系中,用列表描点法作出抛物线的图象,并根据图象写出x取何值时,函
数值大于零;
(3)将此抛物线的图象向下平移一个单位,请写出平称后图象的函数表达式.

(满分14分)如图(1),矩形ABCD的一边BC在直接  坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(
坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(  ),其中
),其中  .
.
(1)求点E、F的坐标(用含的式子表示);
(2)连接OA,若△OAF是等腰三角形,求  的值;
的值;
(3)如图(2),设抛物线  经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求
经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求  、
、  、
、  的值.
的值. 
(11·十堰)12分)如图,已知抛物线y=x2+bx+c与x轴交于点A(1,0)和点B,与y轴交于点C(0,-3)。
(1)求抛物线的解析式;
(2)如图(1),已知点H(0,-1).问在抛物线上是否存在点G(点G在y轴的左侧),使得S△GHC=S△GHA?若存在,求出点G的坐标,若不存在,请说明理由;
(3)如图(2),抛物线上点D在x轴上的正投影为点E(-2,0),F是OC的中点,连接DF,P为线段BD上的一点,若∠EPF=∠BDF,求线段PE的长.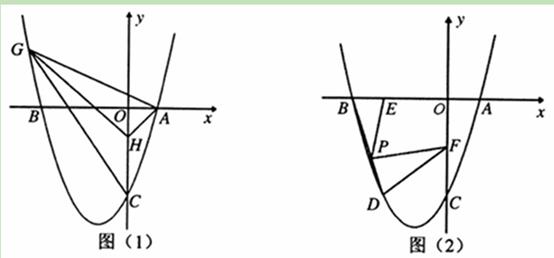
(11·丹东)(本题14分)已知:二次函数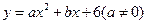 与
与 轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程
轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程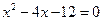 的两个根.
的两个根.
(1)请直接写出点A、点B的坐标.
(2)请求出该二次函数表达式及对称轴和顶点坐标.
(3)如图1,在二次函数对称轴上是否存在点P,使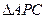 的周长最小,若存在
的周长最小,若存在 ,请求出点P的坐标;若不存在,请说明理由.
,请求出点P的坐标;若不存在,请说明理由.
(4)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合). 过点Q作QD∥AC交于BC点D,设Q点坐标(m,0),当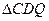 面积S最大时,求m的值.
面积S最大时,求m的值.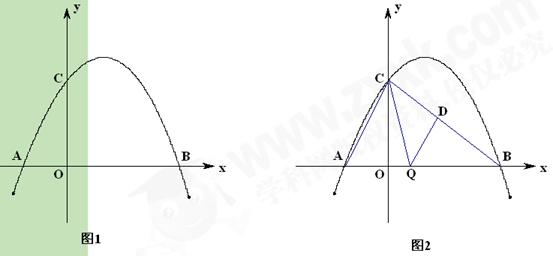
(11·大连)(本题12分)如图15,抛物线y=ax2+bx+c经过A (-1,0)、B (3,
0)、C (0,3)三点,对称轴与抛物线相交于点P、与直线BC相交于点M,连接PB.
(1)求该抛物线的解析式;
(2)抛物线 上是否存在一点Q,使△QMB与△PMB的面积相等,若存在,求点Q的坐标;
上是否存在一点Q,使△QMB与△PMB的面积相等,若存在,求点Q的坐标;
若不存在,说明理由;
(3)在第一象限、对称轴右侧的抛物线上是否存在一点R,使△RPM与△RMB的面积相
等,若存在,直接写出点R的坐标;若不存在,说明理由.
(本小题10分)在平面直角坐标系中,将直线l: 沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线
沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线 :
: 沿x轴平移,得到一条新抛物线
沿x轴平移,得到一条新抛物线 与y轴交于点D,与直线AB交于点E、点F.
与y轴交于点D,与直线AB交于点E、点F.
(Ⅰ)求直线AB的解析式;
(Ⅱ)若线段DF∥x轴,求抛物线 的解析式;
的解析式;
(Ⅲ)在(2)的条件下,若点F在y轴右侧,过F作FH⊥x轴于点G,与直线l交于点H,一条直线m(m不过△AFH的顶点)与AF交于点M,与FH交于点N,如果直线m既垂直于直线AB又平分△AFH的面积,求直线m的解析式.
如图,在平面直角坐标系中,直线AC: 与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c过点A、点C,且与x轴的另一交点为B(x0,0),其中x0>0,又点P是抛物线的对称轴l上一动点.
与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c过点A、点C,且与x轴的另一交点为B(x0,0),其中x0>0,又点P是抛物线的对称轴l上一动点.
(1)求点A的坐标,并在图1中的l上找一点P0,使P0到点A与点C的距离之和最小;
(2)若△PAC周长的最小值为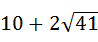 ,求抛物线的解析式及顶点N的坐标;
,求抛物线的解析式及顶点N的坐标;
(3)如图2,在线段CO上有一动点M以每秒2个单位的速度从点C向点O移动(M不与端点C、O重合),过点M作MH∥CB交x轴于点H,设M移动的时间为t秒,试把△P0HM的面积S表示成时间t的函数,当t为何值时,S有最大值,并求出最大值;
(4)在(3)的条件下,当 时,过M作x轴的平行线交抛物线于E、F两点,问:
时,过M作x轴的平行线交抛物线于E、F两点,问:
过E、F、C三点的圆与直线CN能否相切于点C?请证明你的结论.(备用图图3)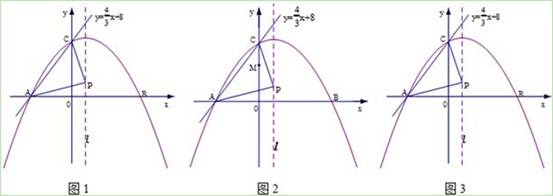
(9分)抛物线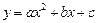 与y轴交于点
与y轴交于点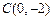 ,与直线
,与直线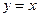
交于点 ,
,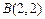 .
.
(1)求抛物线的解析式;
(2)如图,线段MN在线段AB上移动(点M与点A不重合,点N与点B不重合),且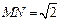 ,若M点的横坐标为m,过点M作
,若M点的横坐标为m,过点M作 x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出m的值;若不能,请说明理由.
x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出m的值;若不能,请说明理由.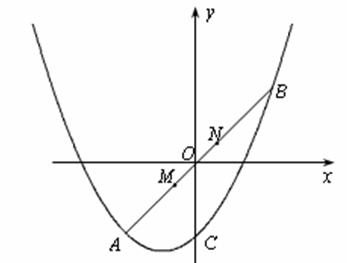
如图,四边形OABC的四个顶点坐标分别为O(0,0),A(8,0),B(4,4),C(0,4),直线l::y=x+b保持与四边形OABC的边交于点M、N(M在折线AOC上,N在折线ABC上)设四边形OABC在l右下方部分的面积为S1,在l左上方部分的面积为S2,记S为的差(S≥0)。
(1)求∠OAB的大小;
(2)当M、N重合时,求l的解析式;
(3)当b≤0时,问线段AB上是否存在点N使得S=0?若存在,求b的值;若不存在,请说明理由;
(4)求S与b的函数关系式。
(本小题满分10分)已知二次函数
(1)当 时,函数值
时,函数值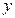 随
随 的增大而减小,求
的增大而减小,求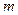 的取值范围。
的取值范围。
(2)以抛物线 的顶点
的顶点 为一个顶点作该抛物线的内接正三角形
为一个顶点作该抛物线的内接正三角形 (
( ,
, 两点在抛物线上),请问:△
两点在抛物线上),请问:△ 的面积是与
的面积是与 无关的定值吗?若是,请求出这个定值;若不是,请说明理由。
无关的定值吗?若是,请求出这个定值;若不是,请说明理由。
(3)若抛物线 与
与 轴交点的横坐标均为整数,求整数
轴交点的横坐标均为整数,求整数 的值。
的值。
(11·肇庆)(本小题满分10分)  .
.
(1)求证:抛物线的对称轴在y轴的左恻:
(3)设抛物线与y轴交于点C,若△ABC是直角三角形.求△ABC的面积.
(本题16分)如图 ,正
,正 比例函数和反比例函数的图象都经过点 A ( 3 , 3) ,把直线 OA 向下平移后,与反比例函数的图象交于点B(6,m),与x轴、y轴分别交于C、D两点。
比例函数和反比例函数的图象都经过点 A ( 3 , 3) ,把直线 OA 向下平移后,与反比例函数的图象交于点B(6,m),与x轴、y轴分别交于C、D两点。
(1)求 m的值;
( 2 )求过 A、B、D 三点的抛物线的解析式;
( 3 )若点E是抛物线上的一个动点,是否存在点 E ,使四边形 OECD 的面积S1,是四边形OACD 面积S的
,使四边形 OECD 的面积S1,是四边形OACD 面积S的 ?若存在,求点 E 的坐标;若不存在,请说明理由.
?若存在,求点 E 的坐标;若不存在,请说明理由.
试题篮
()