初中数学二次函数在给定区间上的最值解答题

（本题10分）已知二次函数的图像与y轴交于点A，且经过点.
（1）求此二次函数的解析式；
（2）将点A沿x轴方向平移，使其落到该函数图像上另一点B处，求点B的坐标.

（本题满分14分，第（1）、（2）小题每小题满分5分，第（3）小题满分4分）
已知，在边长为6的正方形ABCD的两侧如图作正方形BEFG、正方形DMNK，恰好使得N、A、F三点在一直线上，联结MF交线段AD于点P，联结NP，设正方形BEFG的边长为x，正方形DMNK的边长为y，
（1）求y关于x的函数关系式及自变量x的取值范围；
（2）当△NPF的面积为32时，求x的值；
（3）以P为圆心，AP为半径的圆能否与以G为圆心，GF为半径的圆相切，若能请求x的值，若不能，请说明理由。

（本题满分12分，每小题满分各6分）
已知：直角坐标系xoy中，将直线沿y轴向下平移3个单位长度后恰好经过B(-3，0)及y轴上的C点．若抛物线与轴交于A，B两点（点A在点B的右侧），且经过点C，（1）求直线及抛物线的解析式；（2）设抛物线的顶点为，点在抛物线的对称轴上，且，求点的坐标；

(本题14分)如图，在平面直角坐标系中，抛物线与x轴交于A、B两点(A点在B点左侧)，与y轴交于C点，顶点为D.过点C、D的直线与x轴交于E点，以OE为直径画⊙O₁，交直线CD于P、E两点.

(1)求E点的坐标；
(2)联结PO₁、PA.求证:～；
(3) ①以点O₂ (0，m)为圆心画⊙O₂，使得⊙O₂与⊙O₁相切，当⊙O₂经过点C时，求实数m
的值；
②在①的情形下，试在坐标轴上找一点O₃，以O₃为圆心画⊙O₃，使得⊙O₃与⊙O₁、⊙O₂同时相切.直接写出满足条件的点O₃的坐标(不需写出计算过程).

(本题12分)如图，在平面直角坐标系中，等腰梯形OABC，CB//OA，且点A在x轴正半轴上.已知C(2，4)，BC= 4.
(1)求过O、C、B三点的抛物线解析式，并写出顶点坐标和对称轴；
(2)经过O、C、B三点的抛物线上是否存在P点(与原点O不重合)，使得P点到两坐标轴的
距离相等.如果存在，求出P点坐标；如果不存在，请说明理由.

如图，在平面直角坐标系中，抛物线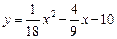与x轴的右交点为点A，与y
轴的交点为点B，过点B作x轴的平行线BC，交抛物线于点C，连结AC．现有两动点P，Q分别从O，C两点同时出发，点P以每秒4个单位的速度沿OA向终点A移动，点Q以每秒1个单位的速度沿CB向点B移动，点P停止运动时，点Q也同时停止运动，线段OC，PQ相交于点D，过点D作DE∥OA，交CA于点E，射线QE交x轴于点F．设动点P，Q移动的时间为t（单位:秒）
（1）求A，B，C三点的坐标和抛物线的顶点的坐标；
（2）当t为何值时，四边形PQCA为平行四边形?
（3）请说明当0＜t＜4.5时，△PQF的面积总为定值；
（4）当0≤t≤4.5是否存在△PQF为等腰三角形？当t为何值时，△PQF为等腰三角形?（直接写出结果）

如图，小明将一张直角梯形纸片沿虚线剪开，得到矩形ABCD和三角形EGF两张纸片，测得AB=5，AD=4，EF=．在进行如下操作时遇到了下面的几个问题，请你帮助解决．

(1) 请你求出FG的长度．
(2)在(1)的条件下，小明先将三角形的边EG和矩形边AB重合，然后将△EFG沿直线BC向右平移，至F点与B重合时停止．在平移过程中，设G点平移的距离为x，两纸片重叠部分面积为．y，求在平移的整个过程中，y与x的函数关系式，并求当重叠部分面积为10时，平移距离x的值．
(3)在(2)的操作中，小明发现在平移过程中，虽然有时平移的距离不等，但两纸片重叠的面积却是相等的；而有时候平移的距离不等，两纸片重叠部分的面积也 不可能相等．请探索这两种情况下重叠部分面积y的范围(直接写出结果)．

如图24，已知抛物线过点C（3，8），与轴交于A，B两点，与y轴交于点D（0，5）．
(1)求该二次函数的关系式；
(2)求该抛物线的顶点M的坐标，并求四边形ABMD的面积；

如图，二次函数y＝ax²＋bx的图象经过点A（4，0）、B（2，2），连结OB、AB．

（1）求a, b；
（2）将△OAB绕点O按顺时针方向旋转135°得到△，则线段的中点P的坐标为   ▲   ，并判断点P是否在此二次函数的图象上，说明你的理由．

某电子科技公司开发一种新产品．产品投产上市一年来，公司经历了由
初期的亏损到后来逐步盈利的过程（公司对经营的盈亏情况每月最后一天结算1次）．公司
前12个月累积获得的利润y（万元）与销售时间第x（月）之间的函数关系（即前x个月的
利润总和y与x之间的关系）对应的点都在如图所示的图象上．该图象是某二次函数
y=a(x-h)²+k图象的一部分，点A为抛物线的顶点，且点A，B，C的横坐标分别为4，10，
12，点A，B的纵坐标分别为-16，20．
（1）求前12个月该公司累积获得的利润y（万元）与时间第x（月）之间的函数关系式；
（2）分别求出前9个月公司累积获得的利润和10月份一个月内所获得的利润；
（3）在前12个月中，哪个月该公司一个月内所获得的利润最多？最多利润是多少万元？

．(6分) 已知二次函数的图象与y轴交于点A(0，－6)，与x轴的一个交点坐标是B(－2，0)．
(1)求二次函数的关系式，并写出顶点坐标；
(2)将二次函数图象沿x轴向左平移个单位长度，求所得图象对应的函数关系式．

如图，抛物线F：y＝ax²＋bx＋c的顶点为P，抛物线F与轴交于点A，
过点P作PD⊥x轴于点D，平移抛物线F使其经过点A、D得到抛物线F ′：
y＝a′x²＋b′x＋c′，抛物线F ′与x轴的另一个交点为C．
（1）当a＝1，b＝－2，c＝3时，
①写出点D的坐标  ▲ ；②求b: 的值；
（2）若a、b、c满足b²＝ac，探究b: 的值是否为定值？若是定值请求出这个定值；若不是请说明理由．

如图，在直角坐标平面内，为原点，抛物线经过点（，），且顶点（，）在直线上．
（1）求的值和抛物线的解析式；
（2）如在线段上有一点，满足，在轴上有一点（，），联结，且直线与轴交于点．
①求直线的解析式；
②如点M是直线上的一个动点，在x轴上方的平面内有另一点N，且以O、E、M、N为顶点的四边形是菱形，请求出点N的坐标．（直接写出结果，不需要过程．）

已知二次函数y=ax²+bx+c的图象的顶点坐标为 (0，)，且 ac=．
（1）若该函数的图象经过点（-1，-1）．
①求使y＜0成立的x的取值范围．
②若圆心在该函数的图象上的圆与x轴、y轴都相切，求圆心的坐标．
（2）经过A（0，p）的直线与该函数的图象相交于M，N两点，过M，N作x轴的垂线，垂足分别为M₁，N₁，设△MAM₁，△AM₁N₁，△ANN₁的面积分别为s₁，s₂，s₃，是否存在m，使得对任意实数p≠0都有s₂²=ms₁s₃成立，若存在，求出m的值，若不存在，请说明理由．

如图15，抛物线与轴交于两点，与轴交于点，连结，若
（1）求抛物线对应的二次函数的解析式；
（2）在抛物线的对称轴上是否存在点，使若存在，求出点的坐标；若不存在，请说明理由；
（3）如图16所示，连结，是线段上(不与、重合)的一个动点.过点 作直线，交抛物线于点，连结、，设点的横坐标为．当t为何值时，的面积最大？最大面积为多少？