初中数学三角形的五心选择题

已知a，b，c为△ABC的三边长，且满足a²c²-b²c²=a⁴-b⁴，判断△ABC的形状（   ）

A．等腰三角形	B．直角三角形
C．等腰直角三角形	D．等腰三角形或直角三角形

如图，一个多边形纸片按图示的剪法剪去一个内角后，得到一个内角和为2340°的新多边形，则原多边形的边数为（ ）

A．13

B．14

C．15

D．16

腰△ABC纸片（AB=AC）可按图中所示方法折成一个四边形，点A与点B重合，点C与点D重合，请问原等腰△ABC中的∠B=       度．

如图，△ABC是等边三角形，被一平行于BC的矩形所截，AB被截成三等分，则图中阴影部分的面积是△ABC的面积的（ ）

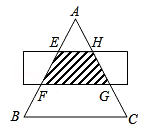
A．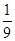

B．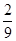

C．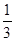

D．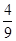

在同一平面内，线段AB=7，BC=3，则AC长为（   ）

A．AC="10"

B．AC=10或4

C．4＜AC＜10

D．4≤AC≤10

若一个多边形的内角和90 0°，则这个多边形的边数为（    ）

A．5

B．7

C．9

D．12

一个多边形的内角和是外角和的2倍，则这个多边形是（   ）

A．四边形

B．五边形

C．六边形

D．八边形

如图，等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上的一点，当PA=CQ时，连接PQ交AC于点D，下列结论中不一定正确的是（ ）

A．PD=DQ

B．DE=AC

C．AE=CQ

D．PQ⊥AB

下列说法中，正确的是（  ）

A．若两条直线被第三条直线所截，则同旁内角互补

B．相等的角是对顶角

C．三角形的外角等于两个内角的和

D．若三条直线两两相交，则共有6对对顶角

一个多边形的每个外角都等于60°，则这个多边形的边数为（ ）

A．8

B．7

C．6

D．5

一个多边形的内角和是360°，这个多边形是（ ）

A．三角形

B．四边形

C．六边形

D．不能确定

如图，等腰三角形ABC中，AB=AC，BD平分∠ABC，∠A=36°，则∠1的度数为（ ）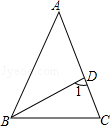

A．36°

B．60°

C．72°

D．108°

正n边形每个内角的大小都为108°，则n=（ ）

A．5

B．6

C．7

D．8

已知三角形两边的长分别是4和10，则此三角形第三边的长可能是（ ）

A．5

B．6

C．12

D．16

如图，在△ABC中，AB=BC，∠ABC=90°，BM是AC边中线，点D，E分别在边AC和BC上，DB=DE，EF⊥AC于点F，以下结论：
（1）∠DBM=∠CDE；
（2）S_△BDE＜S_{四边形BMFE}；
（3）CD•EN=BN•BD；
（4）AC=2DF．
其中正确结论的个数是（ ）．

A．1

B．2

C．3

D．4