如图,在△ABC中,AB=AC,点D、E在BC上,且BD=CE.
求证:△ABE≌△ACD.
如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE, B=
B= E。
E。
求证: ADB=
ADB= FCE.
FCE.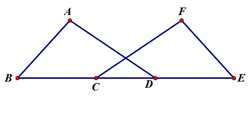
如图,在四边形ABCD中,AB=3cm,BC=4cm,CD=12cm,DA=13cm,∠B=90°.
求四边形ABCD的面积.
如图,在△ABC中,∠B=54°,AD平分∠CAB,交BC于D,E为AC边上一点,连结DE,∠EAD=∠EDA,EF⊥BC于点F.求∠FED的度数.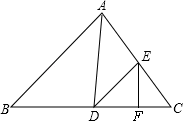
(本小题6分)如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.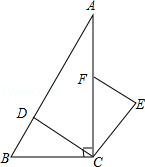
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
已知:如图,在□ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF;
(2)当∠DOE满足什么条件时,四边形BEDF是菱形,说明理由.
如图,在正方形ABCD中AC与BD交于点O,形外有一点E,使∠AED=90°,且DE=3,OE= ,则AE= .
,则AE= .
如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
(本小题满分8分)如下图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.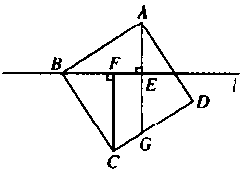
(1)求证:△ABE≌△ABE;
(2)若∠CBF=65°,求∠AGC的度数.
如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD、CE,两线交于点F.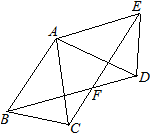
(1)求证:△ABD≌△ACE;
(2)求证:四边形ABFE是菱形.
如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于D,连接DC、DA、OA、OC,四边形OADC为平行四边形。

(1)求证:△BOC≌△CDA
(2)若AB=2,求阴影部分的面积。
如图,在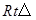 ABC中,∠C=90º,BD是
ABC中,∠C=90º,BD是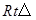 ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,
ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,

(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长
如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.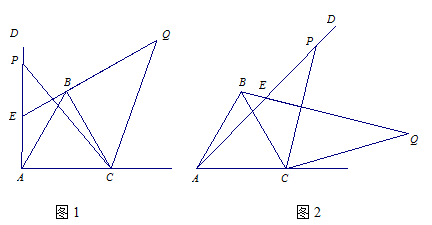
(1)如图1,猜想∠QEP= °;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.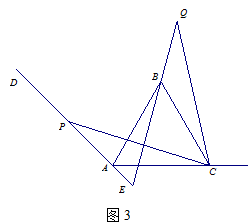
试题篮
()