如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
如图,在 中,
中, ,
, .
.
(1)直接写出 的大小(用含
的大小(用含 的式子表示);
的式子表示);
(2)以点 为圆心、
为圆心、 长为半径画弧,分别交
长为半径画弧,分别交 、
、 于
于 、
、 两点,并连接
两点,并连接 、
、 .若
.若 =30°,求
=30°,求 的度数.
的度数.
如图,直线y= x+2与x轴、y轴分别交于A、B两点,点C的坐标为(﹣3,0),P(x,y)是直线y=
x+2与x轴、y轴分别交于A、B两点,点C的坐标为(﹣3,0),P(x,y)是直线y= x+2的一个动点(点P不与点A重合).
x+2的一个动点(点P不与点A重合).
(1)在点P运动过程中,试写出△OPC的面积S与x的函数关系式;
(2)当P运动到什么位置时,△OPC的面积为 ,求出此时点P的坐标;
,求出此时点P的坐标;
(3)过P作AB的垂线分别交x轴、y轴于E、F两点,是否存在这样的点P,使△EOF≌△BOA?若存在,求出点P的坐标;若不存在,请说明理由.
如图,在△ABC中,∠B=90°,AB=BC=4,点E在BC上,将△ABC沿AE折叠,
使点B落在AC边上的点F处.
(1)求BE的长;
(2)判断△CEF是什么特殊三角形.
已知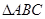 中,
中,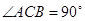 ,
, ,
, .在射线
.在射线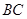 上取一点
上取一点 ,使得
,使得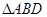 为等腰三角形,这样的三角形有几个?请你求
为等腰三角形,这样的三角形有几个?请你求 的周长.
的周长.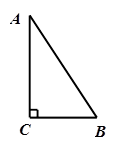
如图,已知直线 :
: 与直线
与直线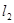 :y = mx-4m的图像的交点C 在第四象限,且点C到y轴的距离为2.
:y = mx-4m的图像的交点C 在第四象限,且点C到y轴的距离为2.
(1)求直线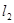 的解析式;
的解析式;
(2)求△ADC的面积;
(3)在第一象限的角平分线上是否存在点P,使得△ADP的面积是△ADC的面积的2倍?如果存在,求出点P的坐标,如果不存在,请说明理由.
如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F,另一边交CB的延长线于点G.
(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变.(1)中的结论是否仍然成立?若成立,情给予证明;若不成立,请说明理由;
已知命题:如图,点A,D,B,E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.
(8分)如图:△ABC中,AD是高,CE是中线,G是CE的中点,DG⊥CE,G为垂足。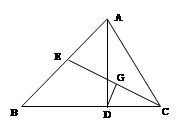
请说明下列结论成立的理由:
(1)DC=BE ; (2)∠B=2∠BCE 。
如图所示,OA=OD,OB=OC,请说明下列结论成立的理由: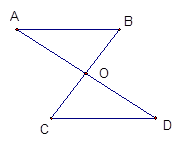
(1)△AOB≌△DOC; (2)AB∥CD
试题篮
()