初中数学三角形的五心计算题

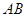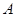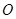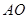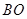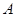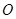（本小题满分8分）如图，梯子斜靠在一竖直的墙上，梯子的底端到墙根的距离为2米，梯子的顶端B到地面的距离为6米．现将梯子的底端向外移动到，使梯子的底端到墙根的距离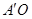等于3米，同时梯子的顶端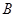下降至．求梯子顶端下滑的距离．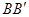

已知：如图，E是BC上一点，AB=EC，AB∥CD，BC=CD．求证：AC=ED．

已知等腰三角形的一边长等于4cm，一边长等于9cm，求它的周长．

已知，如图，DE∥BC，∠A=60°，∠B=50°；

（1）求∠1的度数；
（2）若FH⊥AB于点H，且∠2=∠3，试判断CD与AB的位置关系？并加以证明．

一个零件的形状如图所示，按规定这个零件中∠A和∠DBC都应为直角，工人师傅量出了这个零件各边尺寸，那么这个零件符合要求吗？求出四边形ABCD的面积．

如图，将长方形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E．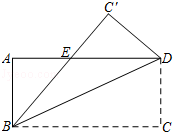

（1）试判断△BDE的形状，并说明理由；
（2）若AB=4，AD=8，求△BDE的面积．

如图，在矩形ABCD中，E、F分别是边AB、CD的中点，连接AF，CE．

（1）求证：△BEC≌△DFA；
（2）求证：四边形AECF是平行四边形．

已知坐标平面内的三个点A（1，3），B（3，1），O（0，0），求△ABO的面积．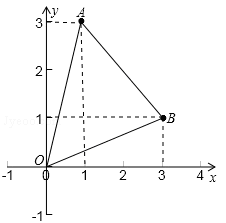

如图，已知EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD的度数，下面给出了求∠AGD的度数的过程，将此补充完整并在括号里填写依据．

解∵EF∥AD（已知）
∴∠2=  （           ）
又∵∠1=∠2（已知）
∴∠1=∠3（等式性质或等量代换）
∴AB∥   （        ）
∴∠BAC+   =180°（          ）
又∵∠BAC=70°（已知）
∴∠AGD=   （     ）

如图，已知在平行四边形ABCD中，E、F分别是边AD、BC上的点，且DE=BF，过E、F两点作直线，分别与CD、AB的延长线相交于点M、N，连接CE、AF．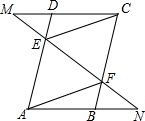

求证：（1）四边形AFCE是平行四边形；
（2）△MEC≌△NFA．

如图，已知四边形ABCD和DEFG都是正方形，连接AE、CG．请猜想AE与CG有什么数量关系？并证明你的猜想．

如图，EF∥BC，AC平分∠BAF，∠B=80°．求∠C的度数．

如图，在四边形ABCD中，AB=AD，AC是∠BAD的角平分线．
求证：△ABC≌△ADC．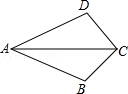

（1）计算：+（π-3）⁰-tan45°；
（2）计算：（）÷．

已知，如图，点B、E、C、F四点在同一条直线上，AB∥DE，AB=DE，AC、DE相交于点O，BE=CF．求证：AC=DF．