初中数学解答题

已知抛物线 G： y＝ mx ²﹣2 mx﹣3有最低点．

（1）求二次函数 y＝ mx ²﹣2 mx﹣3的最小值（用含 m的式子表示）；

（2）将抛物线 G向右平移 m个单位得到抛物线 G ₁．经过探究发现，随着 m的变化，抛物线 G ₁顶点的纵坐标 y与横坐标 x之间存在一个函数关系，求这个函数关系式，并写出自变量 x的取值范围；

（3）记（2）所求的函数为 H，抛物线 G与函数 H的图象交于点 P，结合图象，求点 P的纵坐标的取值范围．

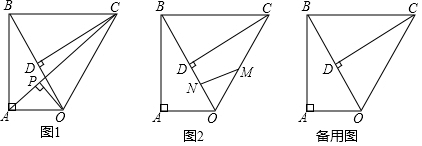
已知Rt△ OAB，∠ OAB＝90°，∠ ABO＝30°，斜边 OB＝4，将Rt△ OAB绕点 O顺时针旋转60°，如图1，连接 BC．

（1）填空：∠ OBC＝ 　　°；

（2）如图1，连接 AC，作 OP⊥ AC，垂足为 P，求 OP的长度；

（3）如图2，点 M， N同时从点 O出发，在△ OCB边上运动， M沿 O→ C→ B路径匀速运动， N沿 O→ B→ C路径匀速运动，当两点相遇时运动停止，已知点 M的运动速度为1.5单位/秒，点 N的运动速度为1单位/秒，设运动时间为 x秒，△ OMN的面积为 y，求当 x为何值时 y取得最大值？最大值为多少？

已知抛物线 $y=a{\left(x-\frac{1}{2}\right)}^2-2$ ，顶点为 A，且经过点 $B\left(-\frac{3}{2},2\right)$ ，点 $C\left(\frac{5}{2},2\right)$ ．

（1）求抛物线的解析式；

（2）如图1，直线 AB与 x轴相交于点 M， y轴相交于点 E，抛物线与 y轴相交于点 F，在直线 AB上有一点 P，若∠ OPM＝∠ MAF，求△ POE的面积；

（3）如图2，点 Q是折线 A﹣ B﹣ C上一点，过点 Q作 QN∥ y轴，过点 E作 EN∥ x轴，直线 QN与直线 EN相交于点 N，连接 QE，将△ QEN沿 QE翻折得到△ QEN ₁，若点 N ₁落在 x轴上，请直接写出 Q点的坐标．

如图，在四边形 ABCD中，∠ B＝60°，∠ D＝30°， AB＝ BC．

（1）求∠ A+∠ C的度数；

（2）连接 BD，探究 AD， BD， CD三者之间的数量关系，并说明理由；

（3）若 AB＝1，点 E在四边形 ABCD内部运动，且满足 AE ²＝ BE ²+ CE ²，求点 E运动路径的长度．

如图，在▱ OABC中， A、 C两点的坐标分别为（4，0）、（﹣2，3），抛物线 W经过 O、 A、 C三点，点 D是抛物线 W的顶点．

（1）求抛物线 W的函数解析式及顶点 D的坐标；

（2）将抛物线 W和▱ OABC同时先向右平移4个单位长度，再向下平移 m（0＜ m＜3）个单位长度，得到抛物线 W ₁和□ O ₁ A ₁ B ₁ C ₁，在向下平移过程中， O ₁ C ₁与 x轴交于点 H，▱ O ₁ A ₁ B ₁ C ₁与▱ OABC重叠部分的面积记为 S，试探究：当 m为何值时， S有最大值，并求出 S的最大值；

（3）在（2）的条件下，当 S取最大值时，设此时抛物线 W ₁的顶点为 F，若点 M是 x轴上的动点，点 N是抛物线 W ₁上的动点，是否存在这样的点 M、 N，使以 D、 F、 M、 N为顶点的四边形是平行四边形？若存在，求出点 M的坐标；若不存在，请说明理由．

已知，如图，抛物线 y＝ ax ²+ bx+ c（ a≠0）的顶点为 M（1，9），经过抛物线上的两点 A（﹣3，﹣7）和 B（3， m）的直线交抛物线的对称轴于点 C．

（1）求抛物线的解析式和直线 AB的解析式．

（2）在抛物线上 A、 M两点之间的部分（不包含 A、 M两点），是否存在点 D，使得 S _{△ DAC}＝2 S _{△ DCM}？若存在，求出点 D的坐标；若不存在，请说明理由．

（3）若点 P在抛物线上，点 Q在 x轴上，当以点 A， M， P， Q为顶点的四边形是平行四边形时，直接写出满足条件的点 P的坐标．

如图，抛物线 y＝ ax ²+ bx﹣2（ a≠0）与 x轴交于 A（﹣3，0）， B（1，0）两点，与 y轴交于点 C，直线 y＝﹣ x与该抛物线交于 E， F两点．

（1）求抛物线的解析式．

（2） P是直线 EF下方抛物线上的一个动点，作 PH⊥ EF于点 H，求 PH的最大值．

（3）以点 C为圆心，1为半径作圆，⊙ C上是否存在点 M，使得△ BCM是以 CM为直角边的直角三角形？若存在，直接写出 M点坐标；若不存在，说明理由．

【问题】

如图1，在Rt△ ABC中，∠ ACB＝90°， AC＝ BC，过点 C作直线 l平行于 AB．∠ EDF＝90°，点 D在直线 l上移动，角的一边 DE始终经过点 B，另一边 DF与 AC交于点 P，研究 DP和 DB的数量关系．

【探究发现】

（1）如图2，某数学兴趣小组运用"从特殊到一般"的数学思想，发现当点 D移动到使点 P与点 C重合时，通过推理就可以得到 DP＝ DB，请写出证明过程；

【数学思考】

（2）如图3，若点 P是 AC上的任意一点（不含端点 A、 C），受（1）的启发，这个小组过点 D作 DG⊥ CD交 BC于点 G，就可以证明 DP＝ DB，请完成证明过程；

【拓展引申】

（3）如图4，在（1）的条件下， M是 AB边上任意一点（不含端点 A、 B）， N是射线 BD上一点，且 AM＝ BN，连接 MN与 BC交于点 Q，这个数学兴趣小组经过多次取 M点反复进行实验，发现点 M在某一位置时 BQ的值最大．若 AC＝ BC＝4，请你直接写出 BQ的最大值．

如图，在平面直角坐标系中，已知抛物线 y＝ ax ²+ bx+2（ a≠0）与 x轴交于 A（﹣1，0）， B（3，0）两点，与 y轴交于点 C，连接 BC．

（1）求该抛物线的解析式，并写出它的对称轴；

（2）点 D为抛物线对称轴上一点，连接 CD、 BD，若∠ DCB＝∠ CBD，求点 D的坐标；

（3）已知 F（1，1），若 E（ x， y）是抛物线上一个动点（其中1＜ x＜2），连接 CE、 CF、 EF，求△ CEF面积的最大值及此时点 E的坐标．

（4）若点 N为抛物线对称轴上一点，抛物线上是否存在点 M，使得以 B， C， M， N为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点 M的坐标；若不存在，请说明理由．

如图，已知抛物线 y＝ ax ²﹣2 x+ c经过△ ABC的三个顶点，其中点 A（0，1），点 B（9，10）， AC∥ x轴．

（1）求这条抛物线的解析式；

（2）求tan∠ ABC的值；

（3）若点 D为抛物线的顶点，点 E是直线 AC上一点，当△ CDE与△ ABC相似时，求点 E的坐标．

如图，抛物线 y＝ ax ²+ bx﹣5与坐标轴交于 A（﹣1，0）， B（5，0）， C（0，﹣5）三点，顶点为 D．

（1）请直接写出抛物线的解析式及顶点 D的坐标；

（2）连接 BC与抛物线的对称轴交于点 E，点 P为线段 BC上的一个动点（点 P不与 B、 C两点重合），过点 P作 PF∥ DE交抛物线于点 F，设点 P的横坐标为 m．

①是否存在点 P，使四边形 PEDF为平行四边形？若存在，求出点 P的坐标；若不存在，说明理由．

②过点 F作 FH⊥ BC于点 H，求△ PFH周长的最大值．

某市计划在十二年内通过公租房建设，解决低收入人群的住房问题．已知前7年，每年竣工投入使用的公租房面积 y（单位：百万平方米），与时间 x（第 x年）的关系构成一次函数，（1≤ x≤7且 x为整数），且第一和第三年竣工投入使的公租房面积分别为 $\frac{23}{6}$ 和 $\frac{7}{2}$ 百万平方米；后5年每年竣工投入使用的公租房面积 y（单位：百万平方米），与时间 x（第 x年）的关系是 y＝﹣ $\frac{1}{8}$x+ $\frac{15}{4}$ （7＜ x≤12且 x为整数）．

（1）已知第6年竣工投入使用的公租房面积可解决20万人的住房问题，如果人均住房面积，最后一年要比第6年提高20%，那么最后一年竣工投入使用的公租房面积可解决多少万人的住房问题？

（2）受物价上涨等因素的影响，已知这12年中，每年竣工投入使用的公租房的租金各不相同，且第一年，一年38元/ m ²，第二年，一年40元/ m ²，第三年，一年42元/ m ²，第四年，一年44元/ m ²……以此类推，分析说明每平方米的年租金和时间能否构成函数，如果能，直接写出函数解析式；

（3）在（2）的条件下，假设每年的公租房当年全部出租完，写出这12年中每年竣工投入使用的公租房的年租金 W关于时间 x的函数解析式，并求出 W的最大值（单位：亿元）．如果在 W取得最大值的这一年，老张租用了58 m ²的房子，计算老张这一年应交付的租金．

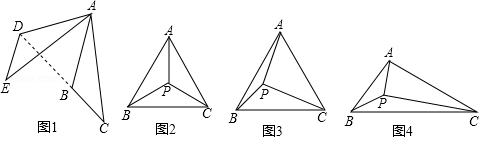
（1）【操作发现】

如图1，将△ ABC绕点 A顺时针旋转60°，得到△ ADE，连接 BD，则∠ ABD＝ 　　度．

（2）【类比探究】

如图2，在等边三角形 ABC内任取一点 P，连接 PA， PB， PC，求证：以 PA， PB， PC的长为三边必能组成三角形．

（3）【解决问题】

如图3，在边长为 $\sqrt{7}$ 的等边三角形 ABC内有一点 P，∠ APC＝90°，∠ BPC＝120°，求△ APC的面积．

（4）【拓展应用】

如图4是 A， B， C三个村子位置的平面图，经测量 AC＝4， BC＝5，∠ ACB＝30°， P为△ ABC内的一个动点，连接 PA， PB， PC．求 PA+ PB+ PC的最小值．

已知抛物线 y＝﹣ $\frac{1}{2}$x ²﹣ $\frac{3}{2}$x的图象如图所示：

（1）将该抛物线向上平移2个单位，分别交 x轴于 A、 B两点，交 y轴于点 C，则平移后的解析式为 　　．

（2）判断△ ABC的形状，并说明理由．

（3）在抛物线对称轴上是否存在一点 P，使得以 A、 C、 P为顶点的三角形是等腰三角形？若存在，求出点 P的坐标；若不存在，说明理由．

如图，在平面直角坐标系中，已知抛物线 y＝ $\frac{1}{2}$x ²+ $\frac{3}{2}$x﹣2与 x轴交于 A， B两点（点 A在点 B的左侧），与 y轴交于点 C，直线 l经过 A， C两点，连接 BC．

（1）求直线 l的解析式；

（2）若直线 x＝ m（ m＜0）与该抛物线在第三象限内交于点 E，与直线 l交于点 D，连接 OD．当 OD⊥ AC时，求线段 DE的长；

（3）取点 G（0，﹣1），连接 AG，在第一象限内的抛物线上，是否存在点 P，使∠ BAP＝∠ BCO﹣∠ BAG？若存在，求出点 P的坐标；若不存在，请说明理由．