初中数学解答题

如图，抛物线 y＝ ax ²+ bx+2与 x轴相交于 A（﹣1，0）， B（4，0）两点，与 y轴相交于点 C．

（1）求抛物线的解析式；

（2）将△ ABC绕 AB中点 M旋转180°，得到△ BAD．

①求点 D的坐标；

②判断四边形 ADBC的形状，并说明理由；

（3）在该抛物线对称轴上是否存在点 P，使△ BMP与△ BAD相似？若存在，请求出所有满足条件的 P点的坐标；若不存在，请说明理由．

如图1，在平面直角坐标系xOy中，点A的坐标为（0，1），取一点B（b，0），连接AB，作线段AB的垂直平分线l₁，过点B作x轴的垂线l₂，记l₁，l₂的交点为P．

（1）当b＝3时，在图1中补全图形（尺规作图，不写作法，保留作图痕迹）；

（2）小慧多次取不同数值b，得出相应的点P，并把这些点用平滑的曲线连接起来发现：这些点P竟然在一条曲线L上！

①设点P的坐标为（x，y），试求y与x之间的关系式，并指出曲线L是哪种曲线；

②设点P到x轴，y轴的距离分别是d₁，d₂，求d₁+d₂的范围，当d₁+d₂＝8时，求点P的坐标；

③将曲线L在直线 $y＝2$下方的部分沿直线y＝2向上翻折，得到一条“W”形状的新曲线，若直线 $y＝\mathit{kx}+3$与这条“W”形状的新曲线有4个交点，直接写出k的取值范围．

如图所示，已知抛物线 $y＝a（x+3\mathit{）（}x﹣1\mathit{）（}a\ne 0）$，与x轴从左至右依次相交于A、B两点，与y轴相交于点C，经过点A的直线 $y=-\sqrt{3}+b$与抛物线的另一个交点为D．

（1）若点D的横坐标为2，求抛物线的函数解析式；

（2）若在第三象限内的抛物线上有点P，使得以A、B、P为顶点的三角形与△ABC相似，求点P的坐标；

（3）在（1）的条件下，设点E是线段AD上的一点（不含端点），连接BE．一动点Q从点B出发，沿线段BE以每秒1个单位的速度运动到点E，再沿线段ED以每秒 $\frac{2\sqrt{3}}{3}$个单位的速度运动到点D后停止，问当点E的坐标是多少时，点Q在整个运动过程中所用时间最少？

如图1，在平面直角坐标系xOy中，抛物线 $y＝a{x}^2+1$经过点 $A（4\mathit{，﹣}3）$，顶点为点B，点P为抛物线上的一个动点，l是过点（0，2）且垂直于y轴的直线，过P作PH⊥l，垂足为H，连接PO．

（1）求抛物线的解析式，并写出其顶点B的坐标；

（2）①当P点运动到A点处时，计算：PO＝　　，PH＝　　，由此发现，PO　　PH（填“＞”、“＜”或“＝”）；

②当P点在抛物线上运动时，猜想PO与PH有什么数量关系，并证明你的猜想；

（3）如图2，设点C（1，﹣2），问是否存在点P，使得以P，O，H为顶点的三角形与△ABC相似？若存在，求出P点的坐标；若不存在，请说明理由．

阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M（1，3）的特征线有： $x＝1$， $y＝3$， $y＝x+2$， $y\mathit{＝﹣}x+4$．

问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线 $y=\frac{1}{4}{(x-m)}^2+n$经过B、C两点，顶点D在正方形内部．

（1）直接写出点D（m，n）所有的特征线；

（2）若点D有一条特征线是y＝x+1，求此抛物线的解析式；

（3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于坐标轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？

如图，直线 $y=-\sqrt{3}x+2\sqrt{3}$与x轴，y轴分别交于点A，点B，两动点D，E分别从点A，点B同时出发向点O运动（运动到点O停止），运动速度分别是1个单位长度/秒和 $\sqrt{3}$个单位长度/秒，设运动时间为t秒，以点A为顶点的抛物线经过点E，过点E作x轴的平行线，与抛物线的另一个交点为点G，与AB相交于点F．

（1）求点A，点B的坐标；

（2）用含t的代数式分别表示EF和AF的长；

（3）当四边形ADEF为菱形时，试判断△AFG与△AGB是否相似，并说明理由．

（4）是否存在t的值，使△AGF为直角三角形？若存在，求出这时抛物线的解析式；若不存在，请说明理由．

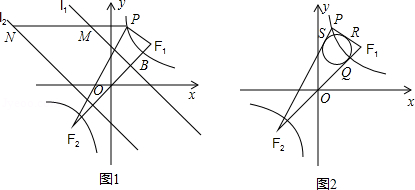
如图1所示，已知：点A（﹣2，﹣1）在双曲线 $\text{C:}y=\frac{a}{x}$上，直线l₁：y＝﹣x+2，直线l₂与l₁关于原点成中心对称，F₁（2，2），F₂（﹣2，﹣2）两点间的连线与曲线C在第一象限内的交点为B，P是曲线C上第一象限内异于B的一动点，过P作x轴平行线分别交l₁，l₂于M，N两点．

（1）求双曲线C及直线l₂的解析式；

（2）求证： $P{F}_2﹣P{F}_1＝\mathit{MN}＝4$；

（3）如图2所示，△PF₁F₂的内切圆与F₁F₂，PF₁，PF₂三边分别相切于点Q，R，S，求证：点Q与点B重合．（参考公式：在平面坐标系中，若有点A（x₁，y₁），B（x₂，y₂），则A、B两点间的距离公式为 $\mathit{AB}=\sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2}$.

如图，抛物线 $y=-\frac{1}{2}{x}^2+\frac{3}{2}x+2$与x轴交于点A，点B，与y轴交于点C，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．

（1）求点A、点B、点C的坐标；

（2）求直线BD的解析式；

（3）当点P在线段OB上运动时，直线l交BD于点M，试探究m为何值时，四边形CQMD是平行四边形；

（4）在点P的运动过程中，是否存在点Q，使△BDQ是以BD为直角边的直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．

如图，在矩形OABC纸片中，OA＝7，OC＝5，D为BC边上动点，将△OCD沿OD折叠，当点C的对应点落在直线l：y＝﹣x+7上时，记为点E，F，当点C的对应点落在边OA上时，记为点G．

（1）求点E，F的坐标；

（2）求经过E，F，G三点的抛物线的解析式；

（3）当点C的对应点落在直线l上时，求CD的长；

（4）在（2）中的抛物线上是否存在点P，使以E，F，P为顶点的三角形是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

如图，在平面直角坐标系xOy中，直线y＝2x+4与y轴交于A点，与x轴交于B点，抛物线 $C_1:y=-\frac{1}{4}{x}^2+\mathit{bx}+c$过A、B两点，与x轴另一交点为C．

（1）求抛物线解析式及C点坐标．

（2）向右平移抛物线C₁，使平移后的抛物线C₂恰好经过△ABC的外心，抛物线C₁、C₂相交于点D，求四边形AOCD的面积．

（3）已知抛物线C₂的顶点为M，设P为抛物线C₁对称轴上一点，Q为抛物线C₁上一点，是否存在以点M、Q、P、B为顶点的四边形为平行四边形？若存在，直接写出P点坐标；不存在，请说明理由．

如图，矩形OABC的两边OA，OC分别在x轴和y轴的正半轴上，点B的坐标为（ $4\sqrt{3},4$），点D在CB上，且CD：DB＝2：1，OB交AD于点E．平行于x轴的直线l从原点O出发，以每秒1个单位长度的速度沿y轴向上平移，到C点时停止；l与线段OB，AD分别相交与M，N两点，以MN为边作等边△MNP（点P在线段MN的下方）．设直线l的运动时间为t（秒），△MNP与△OAB重叠部分的面积为S（平分单位）．

（1）直接写出点E的坐标；

（2）求S与t的函数关系式；

（3）是否存在某一时刻t，使得 $S=\frac{1}{2}{S}_{\mathit{\Delta ABD}}$成立？若存在，请求出此时t的值；若不存在，请说明理由．

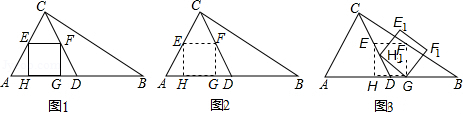
如图1，在△ ABC中，∠ ACB＝90°，∠ B＝30°， AC＝4， D是 AB的中点， EF是△ ACD的中位线，矩形 EFGH的顶点都在△ ACD的边上．

（1）求线段 EF、 FG的长；

（2）如图2，将矩形 EFGH沿 AB向右平移，点 F落在 BC上时停止移动，设矩形移动的距离为 x，矩形与△ CBD重叠部分的面积为 S，求出 S关于 x的函数解析式；

（3）如图3，矩形 EFGH平移停止后，再绕点 G按顺时针方向旋转，当点 H落在 CD边上时停止旋转，此时矩形记作 E ₁ F ₁ GH ₁，设旋转角为α，求cosα的值．

已知二次函数 y＝ ax ²﹣2 ax+ c（ a＜0）的最大值为4，且抛物线过点（ $\frac{7}{2}$ ，﹣ $\frac{9}{4}$ ，点 P（ t，0）是 x轴上的动点，抛物线与 y轴交点为 C，顶点为 D．

（1）求该二次函数的解析式，及顶点 D的坐标；

（2）求| PC﹣ PD|的最大值及对应的点 P的坐标；

（3）设 Q（0，2 t）是 y轴上的动点，若线段 PQ与函数 y＝ a| x| ²﹣2 a| x|+ c的图象只有一个公共点，求 t的取值．

在平面直角坐标系 xOy中，抛物线 y＝ ax ²+ bx+2过点 A（﹣2，0）， B（2，2），与 y轴交于点 C．

（1）求抛物线 y＝ ax ²+ bx+2的函数表达式；

（2）若点 D在抛物线 y＝ ax ²+ bx+2的对称轴上，求△ ACD的周长的最小值；

（3）在抛物线 y＝ ax ²+ bx+2的对称轴上是否存在点 P，使△ ACP是直角三角形？若存在直接写出点 P的坐标，若不存在，请说明理由．

在平面直角坐标系 xOy中，抛物线 y＝ ax ²+ bx+ c与 y轴交于点 C，其顶点记为 M，自变量 x＝﹣1和 x＝5对应的函数值相等．若点 M在直线 l： y＝﹣12 x+16上，点（3，﹣4）在抛物线上．

（1）求该抛物线的解析式；

（2）设 y＝ ax ²+ bx+ c对称轴右侧 x轴上方的图象上任一点为 P，在 x轴上有一点 A（﹣ $\frac{7}{2}$ ，0），试比较锐角∠ PCO与∠ ACO的大小（不必证明），并写出相应的 P点横坐标 x的取值范围．

（3）直线 l与抛物线另一交点记为 B， Q为线段 BM上一动点（点 Q不与 M重合）．设 Q点坐标为（ t， n），过 Q作 QH⊥ x轴于点 H，将以点 Q， H， O， C为顶点的四边形的面积 S表示为 t的函数，标出自变量 t的取值范围，并求出 S可能取得的最大值．