(本题12分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴相交于点A(-3,0),与y轴交于点B,且与正比例函数y=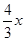 的图象交点为C(m,4)求:
的图象交点为C(m,4)求: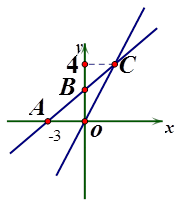
(1)一次函数y=kx+b的解析式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,直接写出点D的坐标。
(3)在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标.
(本题12分)为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了统计表和统计图:
甲、乙射击成绩统计表
| 平均数 |
中位数 |
方差 |
命中10环的次数 |
|
| 甲 |
7 |
0 |
||
| 乙 |
1 |
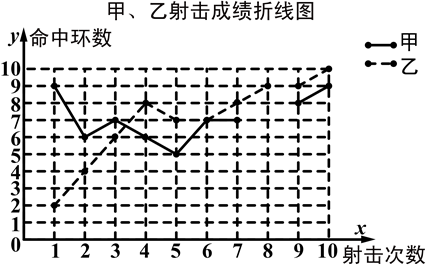
(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
(本题14分)已知:如图,在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD的边AB、BC、DA上,AE=2.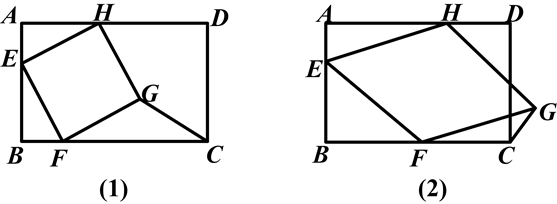
(1)如图(1),当四边形EFGH为正方形时,求△GFC的面积.
(2)如图(2),当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用含a的代数式表示).
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
(本题12分)某班将举行“庆祝建党90周年知识竞赛“活动,班长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:
请根据上面的信息.解决问題:
(1)试计算两种笔记本各买了多少本?
(2)请你解释:小明为什么不可能找回68元?
(本题10分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC和△DEF的顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC向上平移4个单位长度后所得到的△A1B1C1;
(2)画出△DEF绕点O按顺时针方向旋转90°后所得到的△D1E1F1;
(3)△A1B1C1和△D1E1F1组成的图形是轴对称图形吗?如果是,请画出对称轴.
(本题9分)某社区要调查社区居民双休日的学习状况,采用下列调查方式:
①从一幢高层住宅楼中选取200名居民;
②从不同住宅楼中随机选取200名居民;
③选取社区内200名在校学生.
(1)上述调查方式最合理的是 ;
(2)将最合理的调查方式得到的数据制成扇形统计图(如图1)和频数分布直方图(如图2),在这个调查中,200名居民双休日在家学习的有 人;
(3)请估计该社区2 000名居民双休日学习时间不少于4小时的人数.
(本题10分)古希腊著名的毕达哥拉斯学派把1、3、6、10 …,这样的数称为“三角形数”,而把1、4、9、16…,这样的数称为“正方形数”.
(1)第5个三角形数是 ,第n个“三角形数”是 ,第5个“正方形数”是 ,第n个正方形数是 ;
(2)经探究我们发现:任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.
例如:①4=1+3,②9=3+6,③16=6+10,④ ,⑤ ,….
请写出上面第4个和第5个等式;
(3)在(2)中,请探究第n个等式,并证明你的结论.
(本题12分)南水北调工程中线已经在12月27日开始向北京、天津等地供水.为了进一步加强居民的节水意识,合理调配水资源,某区决定对本区的居民用水实行额定用水管理。为了更好的确定额定用水的用水量,首先对本区居民的目前生活用水量进行了入户调查.下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨).
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
(1)请你将调查数据进行如下整理:频数分布表
| 分组 |
划记(用正字划记) |
频数 |
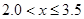 |
||
 |
||
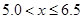 |
||
 |
||
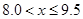 |
||
| 合计 |
(2)结合整理的数据完成频数分布直方图,通过观察直方图你可以得到哪些信息?请你写出你得到的信息.
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定多少吨?
商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价 进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案.
进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案.
(本小题满分7分)如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.已知公路运价为1.5元/(吨•千米),铁路运价为1.2元/(吨•千米),这两次运输共支出公路运输费15000元,铁路运输费97200元.请计算这批产品的销售款比原料费和运输费的和多多少元?
(1)根据题意,某同学列出尚不完整的方程组如下: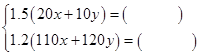 根据这位同学所列方程组,请你指出未知数x,y哪一个代表产品的质量,哪一个代表原料的重量:(注:x、y的单位均为吨),x表示 ,y表示 ;
根据这位同学所列方程组,请你指出未知数x,y哪一个代表产品的质量,哪一个代表原料的重量:(注:x、y的单位均为吨),x表示 ,y表示 ;
(2)在(1)中等式右边的括号里补全所列方程组;
(3)根据他所列方程组解得x=300,请你帮他解出y的值,并解决该实际问题.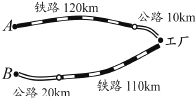
(本题12分)已知, ∥
∥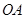 ,
, ,试解答下列问题:
,试解答下列问题:
(1)如图所示,则 ___________°,并判断OB与AC平行吗?为什么?
___________°,并判断OB与AC平行吗?为什么?
(2)如图,若点 在线段
在线段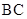 上,且满足
上,且满足 ,并且
,并且 平分
平分 .则
.则 的度数等于_____________°;
的度数等于_____________°;
(3)在第(2)题的条件下,若平行移动 ,如图.
,如图.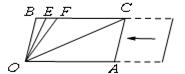
①求 :
: 的值;
的值;
②当 时,求
时,求 的度数(直接写出答案,不必写出解答过程).
的度数(直接写出答案,不必写出解答过程).
(本题11分)一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为3+(-2)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1};
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图(1)中画出四边形OABC;
(3)如图(2),一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
(本题12分)如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =70°.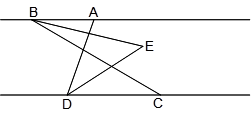
(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
甲、乙、丙三个班向希望工程捐赠图书.已知甲班1人捐6册,有2人各捐7册,其余人各捐11册;乙班有1人捐6册,3人各捐8册,其余人各捐10册;丙班有2人各捐4册,6人各捐7册,其余人各捐9册.已知甲班捐书总数比乙班多28册,乙班比丙班多101册.各班捐书总数都在400册与550册之间.问:每班各有多少人?
试题篮
()