如图,一段抛物线 为 ,与 轴交于 两点,顶点为 ;将 绕点 旋转 得到 ,顶点为 与 组成一个新的图象,垂直于 轴的直线 与新图象交于点 ,与线段 交于点 ,设 均为正数, ,则 的取值范围是( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在矩形 中, ,把边 沿对角线 平移,点 分别对应点 .给出下列结论:①顺次连接点 的图形是平行四边形;②点 到它关于直线 的对称点的距离为 ;③ 的最大值为 ;④ 的最小值为 .其中正确结论的个数是( )

| A. |
个 |
B. |
个 |
C. |
个 |
D. |
个 |
设在一个宽度为 的小巷内搭梯子,梯子的脚位于 点,小巷两边的墙体垂直于水平的地面.将梯子的顶端放于一堵墙的 点时, 离开地面的高度为 ,梯子的倾斜角为 ,将该梯子的顶端放于另一堵墙的 点时, 离开地面的高度为 ,梯子的倾斜角为 ,则小巷的宽度 等于( )
| A. |
|
B. |
|
C. |
|
D. |
|
设 是 的三边长,二次函数 在 取最小值 ,则 是( )
| A. |
等腰三角形 |
B. |
锐角三角形 |
C. |
钝角三角形 |
D. |
直角三角形 |
如图,在平面直角坐标系中,菱形 的边 轴,垂足为 ,顶点 在第二象限,顶点 在 轴正半轴上,反比例函数 的图象同时经过顶点 .若点 的横坐标为 ,则 的值为( )

| A. |
|
B. |
|
C. |
|
D. |
|
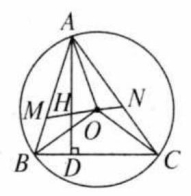
如图,已知 中, 是 的外接圆, 是 边上的高, 是 的垂心,连接 ,连接 并延长交 于点 ,交 于点 ,求证:
(1) ;
(2) 等于 外接圆半径;
(3) .
如图,直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过 两点.
(1)求抛物线的解析式;
(2)如图,点 是直线 上方抛物线上的一动点,当 面积最大时,请求出点 的坐标和 面积的最大值?

如图,点 是等边三角形 内一点,且 ,若将 绕着点 逆时针旋转后得到 .
(1)求点 与点 之间的距离;
(2)求 的度数.

两个水管同时开始向一个空容器内注水.如图是 两个水管各自的注水量 与注水时间 之间的函数图象,已知 水管的注水速度是 , 小时后, 水管的注水量随时间的变化是一段抛物线,其顶点是 ,且注水 小时,容器刚好注满.请根据图象所提供的信息解答下列问题:
(1)直接写出 注水量 与注水时间 之间的函数解解析式,并注明自变量的取值范围;
__________( ),
(2)求容器的容量;
(3)根据图象,通过计算回答,当 时,直接写出 的取值范围.

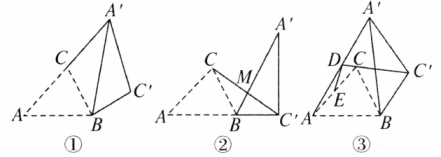
在Rt 中, ,将 绕点 顺时针旋转得到 ,其中点 的对应点分别为点 .
(1)如图①,当点 落在 的延长线上时,求 的长;
(2)如图②,当点 落在 的延长线上时,连接 交 于点 ,求 的长;
(3)如图③,连接 ,直线 交 于点 ,点 为 的中点,连接 .在旋转过程中, 是否存在最小值?若存在,求出 的最小值;若不存在,请说明理由.
已知平面直角坐标系中,点 和直线 (其中 不全为0 ,则点 到直线 的距离 可用公式 来计算.
例如:求点 到直线 的距离,因为直线 可化为 ,其中 ,所以点 到直线 的距离为 .根据以上材料,解答下列问题:
(1)求点 到直线 的距离;
(2)在(1)的条件下, 的半径 ,判断 与直线 的位置关系,若相交,设其弦长为 ,求 的值;若不相交,说明理由.
设 为实数,且 ,拋物线 与 轴交于 两点,与 轴交于点 ,且抛物线的顶点在直线 上.若 是直角三角形,则 面积的最大值是_____.
试题篮
()