对于函数 ,若在定义域存在实数
,若在定义域存在实数 ,满足
,满足 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数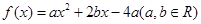 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设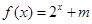 是定义在
是定义在 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围.
的取值范围.
集合M={f(x)|存在实数t使得函数f(x)满足f(t+1)=f(t)+f(1)},则下列函数(a、b、c、k都是常数):
① y=kx+b(k≠0,b≠0);② y=ax2+bx+c(a≠0);
③ y=ax(0<a<1);④ y= (k≠0);⑤ y=sinx.
(k≠0);⑤ y=sinx.
其中属于集合M的函数是________.(填序号)
在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数f(x)的图象恰好通过n(n∈N*)个整点,则称函数f(x)为n阶整点函数.有下列函数:
①f(x)=x+ (x>0);②g(x)=x3;
(x>0);②g(x)=x3;
③h(x)=( )x;④φ()=lnx.
)x;④φ()=lnx.
其中是一阶整点函数的是( )
| A.①②③④ | B.①③④ |
| C.④ | D.①④ |
设f(x)和g(x)都是定义在同一区间上的两个函数,若对任意x∈[1,2],都有|f(x)+g(x)|≤8,则称f(x)和g(x)是“友好函数”,设f(x)=ax,g(x)= .
.
(1)若a∈{1,4},b∈{-1,1,4},求f(x)和g(x)是“友好函数”的概率;
(2)若a∈[1,4],b∈[1,4],求f(x)和g(x)是“友好函数”的概率.
设函数f(x)的定义域为D,若存在非零实数l使得对于任意x∈M(M⊆D),有x+l∈D,且f(x+l)≥f(x),则称函数f(x)为M上的l高调函数.现给出下列命题:
①函数f(x)=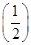 x是R上的1高调函数;
x是R上的1高调函数;
②函数f(x)=sin 2x为R上的π高调函数;
③如果定义域为[-1,+∞)的函数f(x)=x2为[-1,+∞)上的m高调函数,那么实数m的取值范围是[2,+∞).
其中正确的命题是________.(写出所有正确命题的序号)
已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=ex(x+1),给出下列命题:
①当x>0时,f(x)=ex(1-x);②函数f(x)有两个零点;③f(x)>0的解集为(-1,0)∪(1,+∞);④∀x1,x2∈R,都有|f(x1)-f(x2)|<2.
其中正确命题的个数是( )
| A.1 | B.2 |
| C.3 | D.4 |
已知f(x)=32x-(k+1)3x+2,当x∈R时,f(x)恒为正值,则k的取值范围是( )
| A.(-∞,-1) | B.(-∞,2 -1) -1) |
C.(-1,2 -1) -1) |
D.(-2 -1,2 -1,2 -1) -1) |
已知函数①f(x)=x2;②f(x)=ex;③f(x)=ln x;④f(x)=cos x.其中对于f(x)定义域内的任意一个x1都存在唯一的x2,使f(x1)f(x2)=1成立的函数是( )
| A.① | B.② | C.②③ | D.③④ |
已知函数 ,
,
(1)若曲线 与
与 在公共点
在公共点 处有相同的切线,求实数
处有相同的切线,求实数 、
、 的值;
的值;
(2)当 时,若曲线
时,若曲线 与
与 在公共点
在公共点 处有相同的切线,求证:点
处有相同的切线,求证:点 唯一;
唯一;
(3)若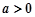 ,
, ,且曲线
,且曲线 与
与 总存在公切线,求正实数
总存在公切线,求正实数 的最小值
的最小值
已知函数
(1)求函数 在点(0,f(0))处的切线方程;
在点(0,f(0))处的切线方程;
(2)求函数 单调递增区间;
单调递增区间;
(3)若
 ∈[1,1],使得
∈[1,1],使得 (e是自然对数的底数),求实数
(e是自然对数的底数),求实数 的取值范围.
的取值范围.
已知函数 的定义域为
的定义域为 ,对定义域内的任意x,满足
,对定义域内的任意x,满足 ,当
,当 时,
时, (a为常),且
(a为常),且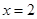 是函数
是函数 的一个极值点,
的一个极值点,
(1)求实数a的值;
(2)如果当 时,不等式
时,不等式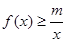 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;
(3)求证:
试题篮
()