设集合A=(―∞,―2]∪[3,+∞),关于x的不等式(x-2a)·(x+a)>0的解集为B(其中a<0).
(1)求集合B;
(2)设p:x∈A,q:x∈B,且Øp是Øq的充分不必要条件,求a的取值范围。
已知P={x|x2﹣8x﹣20≤0},S={x|1﹣m≤x≤1+m}
(1)是否存在实数m,使x∈P是x∈S的充要条件,若存在,求出m的取值范围;
(2)是否存在实数m,使x∈P是x∈S的必要条件,若存在,求出m的取值范围.
已知命题 “存在
“存在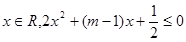 ”,命题
”,命题 :“曲线
:“曲线 表示焦点在
表示焦点在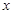 轴上的椭圆”,命题
轴上的椭圆”,命题 “曲线
“曲线 表示双曲线”
表示双曲线”
(1)若“ 且
且 ”是真命题,求
”是真命题,求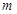 的取值范围;
的取值范围;
(2)若 是
是 的必要不充分条件,求
的必要不充分条件,求 的取值范围。
的取值范围。
设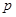 :实数
:实数 满足
满足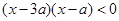 ,其中
,其中 ,
,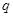 :实数
:实数 满足
满足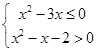 .
.
(1)当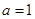 ,
,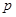 且
且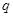 为真时,求实数
为真时,求实数 的取值范围;
的取值范围;
(2)若 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数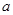 的取值范围.
的取值范围.
(本小题满分12分)设命题p:实数x满足 ,其中
,其中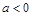 ;命题q:实数
;命题q:实数 满足
满足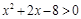 且
且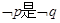 的必要不充分条件,求实数
的必要不充分条件,求实数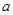 的取值范围.
的取值范围.
数列{xn}满足x1=0,xn+1=-xn2+xn+c(n∈N*).
(1)证明:{xn}是递减数列的充分必要条件是c<0;
(2)求c的取值范围,使{xn}是递增数列.
试题篮
()