(本小题满分12分)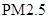 是指空气中直径小于或等于
是指空气中直径小于或等于 微米的颗粒物(也称可入肺颗粒物).为了探究车流量与
微米的颗粒物(也称可入肺颗粒物).为了探究车流量与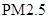 的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与
的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与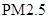 的数据如下表:
的数据如下表:
| 时间 |
周一 |
周二 |
周三 |
周四 |
周五 |
车流量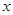 (万辆) (万辆) |
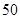 |
 |
 |
 |
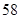 |
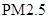 的浓度 的浓度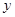 (微克/立方米) (微克/立方米) |
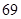 |
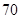 |
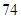 |
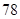 |
 |
(1)根据上表数据,请在下列坐标系中画出散点图;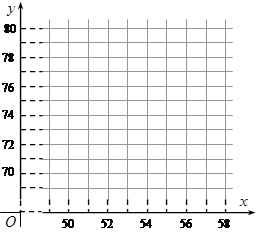
(2)根据上表数据,用最小二乘法求出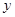 关于
关于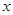 的线性回归方程
的线性回归方程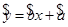 ;
;
(3)若周六同一时间段车流量是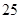 万辆,试根据(2)求出的线性回归方程预测,此时
万辆,试根据(2)求出的线性回归方程预测,此时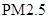 的浓度为多少(保留整数)?
的浓度为多少(保留整数)?
科研人员研究某物质的溶解度 与温度
与温度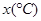 之间的关系,得到如下表部分数据,则其回归直线方程为 (
之间的关系,得到如下表部分数据,则其回归直线方程为 (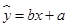 ,其中
,其中 ).
).
温度 (℃) (℃) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
溶解度 |
90 |
84 |
83 |
80 |
75 |
68 |
[2013·福建高考]已知x与y之间的几组数据如下表:
| x |
1 |
2 |
3 |
4 |
5 |
6 |
| y |
0 |
2 |
1 |
3 |
3 |
4 |
假设根据上表数据所得线性回归直线方程为 =
= x+
x+ .若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
.若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
A. >b′,
>b′, >a′ B.
>a′ B. >b′,
>b′, <a′
<a′
C. <b′,
<b′, >a′ D.
>a′ D. <b′,
<b′, <a′
<a′
[2013·杭州模拟]在2013年3月15日,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x和销售量y之间的一组数据如下表所示:
| 价格x(元) |
9 |
9.5 |
10 |
10.5 |
11 |
| 销售量y(件) |
11 |
10 |
8 |
6 |
5 |
由散点图可知,销售量y与价格x之间有较好的线性相关关系,且回归直线方程是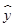 =-3.2x+
=-3.2x+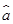 ,则
,则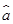 =( )
=( )
A.-24 B.35.6 C.40.5 D.40
一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度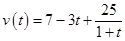 (
( 的单位:
的单位: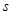 ,
, 的单位:
的单位: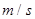 )行驶至停止.在此期间汽车继续行驶的距离(单位:
)行驶至停止.在此期间汽车继续行驶的距离(单位: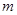 )是( ).
)是( ).
A.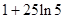 |
B. |
C.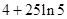 |
D. |
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.根据收集到的数据(如下表),由最小二乘法示得回归直线方程为 。
。
零件数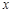 (个) (个) |
10 |
20 |
30 |
40 |
50 |
加工时间 |
62 |
|
75 |
81 |
89 |
表中有一个数据模糊不清,经推断,该数据的值为 .
以下是某地搜集到的新房屋的销售价格 (万元)和房屋的面积
(万元)和房屋的面积 (
( )的数据 ,若由资料可知
)的数据 ,若由资料可知 对
对 呈线性相关关系。
呈线性相关关系。
试求:(1)线性回归方程;
(2)根据(1)的结果估计当房屋面积为 时的销售价格.
时的销售价格.
参考公式:
对于函数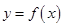 ,部分
,部分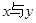 的对应关系如下表:
的对应关系如下表:
数列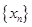 满足:
满足: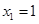 ,且对于任意
,且对于任意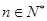 ,点
,点 都在函数
都在函数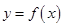 的图象上,则
的图象上,则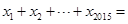 ( )
( )
| A.7539 | B.7546 | C.7549 | D.7554 |
某市电力公司在电力供不应求时期,为了居民节约用电,采用“阶梯电价”方法计算电价,每月用电不超过 度时,按每度
度时,按每度 元计费,每月用电超过
元计费,每月用电超过 度时,超过部分按每度
度时,超过部分按每度 元计费,每月用电超过
元计费,每月用电超过 度时,超过部分按每度
度时,超过部分按每度 元计费.
元计费.
(1)设每月用电 度,应交电费
度,应交电费 元,写出
元,写出 关于
关于 的函数;
的函数;
(2)已知小王家第一季度缴费情况如下:
| 月份 |
1 |
2 |
3 |
合计 |
| 缴费金额 |
87元 |
62元 |
45元8角 |
194元8角 |
问:小王家第一季度共用了多少度电?
下表数据是水温度x(℃)对黄酮延长性y(%)效应的试验结果,y是以延长度计算的,且对于给定的x,y为变量.
| x(℃) |
300 |
400 |
500 |
600 |
700 |
800 |
| y(%) |
40 |
50 |
55 |
60 |
67 |
70 |
(1)求y关于x的回归方程;
(2)估计水温度是1 000 ℃时,黄酮延长性的情况.
(可能用到的公式: ,
, ,其中
,其中 、
、 是对回归直线方程
是对回归直线方程 中系数
中系数 、
、 按最小二乘法求得的估计值)
按最小二乘法求得的估计值)
生产 ,
, 两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 |
 |
 |
 |
 |
 |
元件 |
8 |
12 |
40 |
32 |
8 |
元件 |
7 |
18 |
40 |
29 |
6 |
(Ⅰ)试分别估计元件 、元件
、元件 为正品的概率;
为正品的概率;
(Ⅱ)生产一件元件 ,若是正品可盈利50元,若是次品则亏损10元;生产一件元件
,若是正品可盈利50元,若是次品则亏损10元;生产一件元件 ,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下
,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下
(i)求生产5件元件 所获得的利润不少于300元的概率;
所获得的利润不少于300元的概率;
(ii)记 为生产1件元件
为生产1件元件 和1件元件
和1件元件 所得的总利润,求随机变量
所得的总利润,求随机变量 的分布列和期望.
的分布列和期望.
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作四次试验,得到的数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1)已知零件个数与加工时间线性相关,求出y关于x的线性回归方程;
(2)试预测加工10个零件需要多少时间?
设某中学的女生体重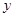 (kg)与身高
(kg)与身高 (cm)具有线性相关关系,根据一组样本数
(cm)具有线性相关关系,根据一组样本数
 ,用最小二乘法建立的线性回归直线方程为
,用最小二乘法建立的线性回归直线方程为 ,给出下列结论,则错误的是( )
,给出下列结论,则错误的是( )
A.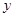 与 与 具有正的线性相关关系 具有正的线性相关关系 |
| B.若该中学某女生身高增加1cm,则其体重约增加0.85kg |
C.回归直线至少经过样本数据  中的一个 中的一个 |
D.回归直线一定过样本点的中心点 |
试题篮
()