在一次考试中,5名同学数学、物理成绩如下表所示:
| 学生 |
A |
B |
C |
D |
E |
| 数学(x分) |
89 |
91 |
93 |
95 |
97 |
| 物理(y分) |
87 |
89 |
89 |
92 |
93 |
(1)根据表中数据,求物理分 对数学分
对数学分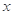 的回归方程:
的回归方程:
(2)要从4名数学成绩在90分以上的同学中选出2名参加一项活动,以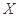 表示选中的同学中物理成绩高于90分的人数,求随机变量
表示选中的同学中物理成绩高于90分的人数,求随机变量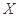 的分布列及数学期望
的分布列及数学期望 .(附:回归方程
.(附:回归方程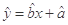 中,
中,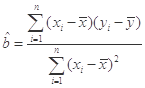 ,
, )
)
由某种设备的使用年限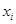 (年)与所支出的维修费
(年)与所支出的维修费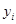 (万元)的数据资料算得如下结果,
(万元)的数据资料算得如下结果,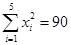 ,
,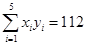 ,
,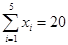 ,
,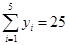 .
.
(1)求所支出的维修费y对使用年限x的线性回归方程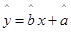 ;
;
(2)①判断变量x与y之间是正相关还是负相关;
②当使用年限为8年时,试估计支出的维修费是多少.
(附:在线性回归方程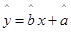 中,)
中,) ,
,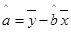 ,其中
,其中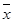 ,
,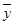 为样本平均值.)
为样本平均值.)
[2013·福建高考]已知x与y之间的几组数据如下表:
| x |
1 |
2 |
3 |
4 |
5 |
6 |
| y |
0 |
2 |
1 |
3 |
3 |
4 |
假设根据上表数据所得线性回归直线方程为 =
= x+
x+ .若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
.若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
A. >b′,
>b′, >a′ B.
>a′ B. >b′,
>b′, <a′
<a′
C. <b′,
<b′, >a′ D.
>a′ D. <b′,
<b′, <a′
<a′
[2013·杭州模拟]在2013年3月15日,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x和销售量y之间的一组数据如下表所示:
| 价格x(元) |
9 |
9.5 |
10 |
10.5 |
11 |
| 销售量y(件) |
11 |
10 |
8 |
6 |
5 |
由散点图可知,销售量y与价格x之间有较好的线性相关关系,且回归直线方程是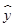 =-3.2x+
=-3.2x+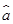 ,则
,则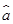 =( )
=( )
A.-24 B.35.6 C.40.5 D.40
以下是某地搜集到的新房屋的销售价格 (万元)和房屋的面积
(万元)和房屋的面积 (
( )的数据 ,若由资料可知
)的数据 ,若由资料可知 对
对 呈线性相关关系。
呈线性相关关系。
试求:(1)线性回归方程;
(2)根据(1)的结果估计当房屋面积为 时的销售价格.
时的销售价格.
参考公式:
某数学兴趣小组有男女生各 名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为
名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为 ,女生数据的平均数为
,女生数据的平均数为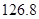 .
.
(1)求 ,
, 的值;
的值;
(2)现从成绩高于 分的同学中随机抽取两名同学,求抽取的两名同学恰好为一男一女的概率.
分的同学中随机抽取两名同学,求抽取的两名同学恰好为一男一女的概率.
对于函数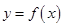 ,部分
,部分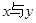 的对应关系如下表:
的对应关系如下表:
数列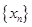 满足:
满足: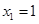 ,且对于任意
,且对于任意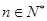 ,点
,点 都在函数
都在函数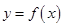 的图象上,则
的图象上,则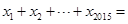 ( )
( )
| A.7539 | B.7546 | C.7549 | D.7554 |
某产品的广告费用与销售额的统计数据如下表
根据上表可得回归方程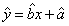 中的
中的 为9.4,据此模型预报广告费用为6万元时
为9.4,据此模型预报广告费用为6万元时
销售额为 ()
| A.63.6万元 | B.65.5万元 | C.67.7万元 | D.72.0万元 |
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?
下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程为=0.7x+0.35,那么表中m值为( ).
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
m |
4 |
4.5 |
A.4 B.3.15 C.4. 5 D.3
设某中学的女生体重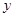 (kg)与身高
(kg)与身高 (cm)具有线性相关关系,根据一组样本数
(cm)具有线性相关关系,根据一组样本数
 ,用最小二乘法建立的线性回归直线方程为
,用最小二乘法建立的线性回归直线方程为 ,给出下列结论,则错误的是( )
,给出下列结论,则错误的是( )
A.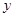 与 与 具有正的线性相关关系 具有正的线性相关关系 |
| B.若该中学某女生身高增加1cm,则其体重约增加0.85kg |
C.回归直线至少经过样本数据  中的一个 中的一个 |
D.回归直线一定过样本点的中心点 |
试题篮
()