高中数学空间向量的应用试题

如图，是圆O的直径，是圆周上不同于的任意一点，平面，则四面体的四个面中，直角三角形的个数有       个．

（满分13分）如图，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA=AB=2a,DC=a,F是BE的中点，


求证：（1）FD∥平面ABC;
（2）AF⊥平面EDB．

如图，在四棱锥中，底面是菱形，且．

（1）求证：；
（2）若平面与平面的交线为，求证：．

如图，在四棱锥中，底面是菱形，且．

（1）求证：；
（2）若平面与平面的交线为，求证：．

在如图所示的几何体中，四边形是等腰梯形，∥，，．在梯形中，∥，且，⊥平面．

（1）求证：；
（2）若二面角为，求的长．

（本小题满分12分）如图所示，在直三棱柱中，AC=BC，D为AB的中点，且

（1）；
（2）证明：平面

（本小题共14分）如图，四边形与均为菱形， ，且．
    
（Ⅰ）求证：平面；
（Ⅱ）求证：∥平面；
（Ⅲ）求二面角的余弦值．

如图，在正方体中，为的中点，点在四边形及其内部运动．若，则点的轨迹为

A．线段

B．圆的一部分

C．椭圆的一部分

D．双曲线的一部分

如图，设四棱锥的底面为菱形，且∠，，。

（1）求证：平面平面；
（2）求平面与平面所夹角的余弦值．

.给出下列结论：
①函数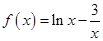在区间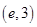上有且只有一个零点；
②已知l是直线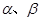，是两个不同的平面.若；
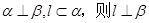③已知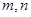表示两条不同直线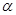，表示平面.若；
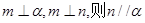④在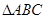中，已知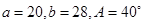，在求边c的长时有两解.
其中所有正确结论的序号是：            .

（本小题满分12分）如图，四棱锥P−ABCD中，底面ABCD为平行四边形，O为AC的中点，PO⊥平面ABCD，M 为PD的中点，∠ADC=45^o，AD=AC =1，PO="a"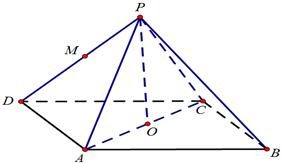

（1）证明：DA⊥平面PAC；
（2）如果二面角M−AC−D的正切值为2，求a的值.

（本小题满分9分）如图所示，四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，M、N分别是AB、PC的中点，PA＝AD＝a．

（1）求证：MN∥平面PAD；
（2）求证：平面PMC⊥平面PCD．

如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD=DE=2AB，F为CD的中点.

（1）求证：平面BCE⊥平面CDE；
（2）求二面角B-EF-D的余弦值.

下列命题中，m、n表示两条不同的直线，α、β、γ表示三个不同的平面．
①若m⊥α，n∥α，则m⊥n；
②若α⊥γ，β⊥γ，则α∥β；
③若m∥α，n∥α，则m∥n；
④若α∥β，β∥γ，m⊥α，则m⊥γ．
则正确的命题是（  ）

A．①③

B．②③

C．①④

D．②④

如图，在直三棱柱中，AB=AC=5，D,E分别为BC, 的中点，四边形是边长为6的正方形.

（1）求证：∥平面；
（2）求证：⊥平面；
（3）求平面与平面的夹角的余弦值.