高中数学空间向量的应用试题

（本小题满分12分）在棱长为2的正方体中，设是棱的中点。

（1）求证：；
（2）求证：平面；
（3）求三棱锥的体积.

如图，四棱锥S-ABCD的底面为正方形，SD⊥底面ABCD， 则下列结论中不正确的是（   ）

A．AC⊥SB

B．AB∥平面SCD

C．AB与SC所成的角等于DC与SA所成的角

D．SA与平面SBD所成的角等于SC与平面SBD所成的角

如图，在三棱柱中，四边形是边长为4的正方形，平面⊥平面，．

（Ⅰ）求证：⊥平面；
（Ⅱ）若点是线段的中点，请问在线段是否存在点，使得面？若存在，请说明点的位置，若不存在，请说明理由；
（Ⅲ）（本小问只理科学生做）求二面角的大小．

（本小题满分14分）如图，在矩形中，,分别为线段、的中点，⊥平面.

（Ⅰ）求证：∥平面；
（Ⅱ）求证：平面⊥平面；

（本小题满分14分）如图，在四棱锥中，面，四边形是正方形，是的中点，是的中点

（1）求证：面；  
（2）求证：面.

是异面直线，下面四个命题：
①过至少有一个平面平行于；
②过至少有一个平面垂直于；
③至多有一条直线与都垂直；
④至少有一个平面与都平行.
其中正确命题的个数是          

如图，在四棱锥中，底面是菱形，且．

（1）求证：；
（2）若平面与平面的交线为，求证：．

（本小题13分）如图，在直三棱柱ABC-A₁B₁C₁中，，点E、F、G分别是AA₁、
AC、BB₁的中点，且CG⊥C₁G .

（1）求证：CG//面BEF;   
（2）求证：面BEF⊥面A₁C₁G .

如下图，在平行四边形ABCD中，AD=2AB=2，∠BAC="90°." 将△ACD沿AC折起，使得BD=. 在三棱锥D-ABC的四个面中，下列关于垂直关系的叙述错误的是（    ）

A．面ABD⊥面BCD	B．面ABD⊥面ACD
C．面ABC⊥面ACD	D．面ABC⊥面BCD

如图所示，为正方体，给出以下五个结论：

①平面；
②⊥平面；
③与底面所成角的正切值是；
④二面角的正切值是；
⑤过点且与异面直线 和 均成70°角的直线有2条．
其中，所有正确结论的序号为________．

（本小题满分12分）如图所示，在直三棱柱ABC-A₁B₁C₁中，AC⊥BC．

（1）求证：平面AB₁C₁⊥平面AC₁；
（2）若AB₁⊥A₁C，求线段AC与AA₁长度之比；
（3）若D是棱CC₁的中点，问在棱AB上是否存在一点E，使DE∥平面AB₁C₁？若存在，试确定点E的位置；若不存在，请说明理由．

（本小题满分12分）如图所示，PA⊥平面ABC，点C在以AB为直径的⊙O上，∠CBA＝30°，PA＝AB＝2，点E为线段PB的中点，点M在AB上，且OM∥AC.

（1）求证：平面MOE∥平面PAC；
（2）求证：平面PAC⊥平面PCB；
（3）设二面角M－BP－C的大小为θ，求的值．

在正四面体P－ABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论中不成立的是

A．BC∥平面PDF

B．DF⊥平面PAE

C．平面PDF⊥平面ABC

D．平面PAE⊥平面ABC

如图，底面是正三角形的直三棱柱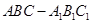中，D是BC的中点，.

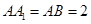（Ⅰ）求证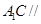：平面；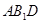
（Ⅱ）求的A₁ 到平面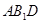的距离.

如图，在四棱锥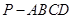中，底面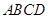是边长为2的菱形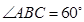，E、F分别是PB、CD的中点，且.

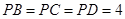（1）求证：；
（2）求证：;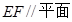
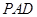（3）求二面角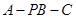的余弦值.