已知四棱锥 的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形. 是侧棱
是侧棱 上的动点.
上的动点.

(1)求证: ;
;
(2)若 为
为 的中点,求直线
的中点,求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3) 若四点 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.
如图,在直三棱柱ABC—A1B1C1中,  ,直线B1C与平面ABC成45°角.
,直线B1C与平面ABC成45°角.
(1)求证:平面A1B1C⊥平面B1BCC1;
(2)求二面角A—B1C—B的余弦值.
已知m和n是两条不同的直线,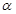 和β是两个不重合的平面,那么下面给出的条件中一定能推出m⊥β的是( )
和β是两个不重合的平面,那么下面给出的条件中一定能推出m⊥β的是( )
A.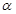 ⊥β且 ⊥β且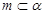 |
B.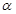 ⊥β且 ⊥β且 |
C. 且n⊥β 且n⊥β |
D.m⊥n且 |
已知下列四个命题,其中真命题的序号是( )
① 若一条直线垂直于一个平面内无数条直线,则这条直线与这个平面垂直;
② 若一条直线平行于一个平面,则垂直于这条直线的直线必垂直于这个平面;
③ 若一条直线平行一个平面,另一条直线垂直这个平面,则这两条直线垂直;
④ 若两条直线垂直,则过其中一条直线有唯一一个平面与另外一条直线垂直;
| A.①② | B.②③ | C.②④ | D.③④ |
已知平面 外不共线的三点
外不共线的三点 到
到 α的距离都相等,则正确的结论是( )
α的距离都相等,则正确的结论是( )
A.平面 必平行于 必平行于 |
B.平面 必与 必与 相交 相交 |
C.平面 必不垂直于 必不垂直于 |
D.存在△ 的一条中位线平行于 的一条中位线平行于 或在 或在 内 内 |
如图,四棱锥 中,侧面
中,侧面 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是 的菱形,
的菱形, 为
为 的中点.
的中点.
(Ⅰ)求 与底面
与底面 所成角的大小;
所成角的大小;
(Ⅱ)求证: 平面
平面 ;(Ⅲ)求二面角
;(Ⅲ)求二面角 的余弦值.
的余弦值.
如图所示,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
(1)求证:DM∥平面APC; (2)求证:平面ABC⊥平面APC.
试题篮
()