如图,三角形
所在的平面与长方形
所在的平面垂直,
,
,
,点
是
的中点,点
、
分别在线段
、
上,且
,
.

(1)证明:
;
(2)求二面角
的正切值;
(3)求直线
与直线
所成角的余弦值.
如图,三棱锥
中,平面
平面
,
,点
在线段
上,且
,点
在线段
上,且
.

(Ⅰ)证明:
平面
.
(Ⅱ)若四棱锥
的体积为7,求线段
的长.
如图,三棱锥 中, 平面 分别为线段 上的点,且

(1)证明: 平面
(2)求二面角 的余弦值。
如图,在三棱锥
中,
在底面
的射影为
的中点,
为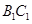
(1)证明:
;
(2)求直线
和平面
所成的角的正弦值.
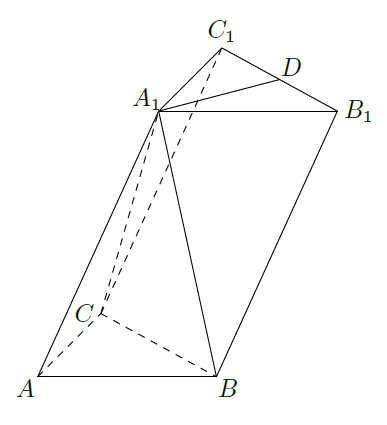
如图,在三棱柱
-中,
,
,
,
在底面
的射影为
的中点,
为
的中点.
(1)证明:
平面
;
(2)求二面角
的平面角的余弦值.
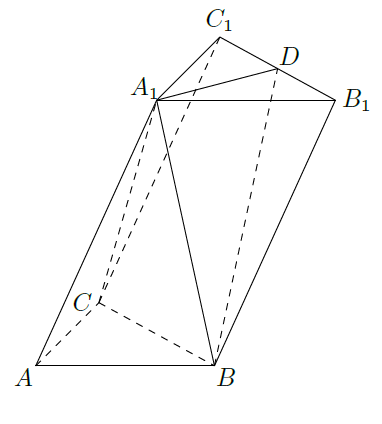
如图,四边形
为菱形,
=120°,
是平面
同一侧的两点,
⊥平面
,
⊥平面
,
,
.
(Ⅰ)证明:平面
⊥平面
;
(Ⅱ)求直线
与直线
所成角的余弦值.
如图,已知
,
,
,
,
,点
分别是
的中点.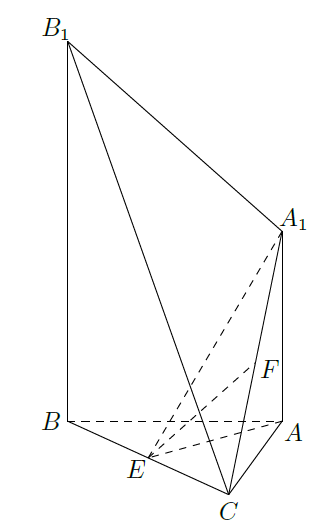
(Ⅰ)求证:
;
(Ⅱ)求证:平面
.
(Ⅲ)求直线
 与平面
所成角的大小.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示:
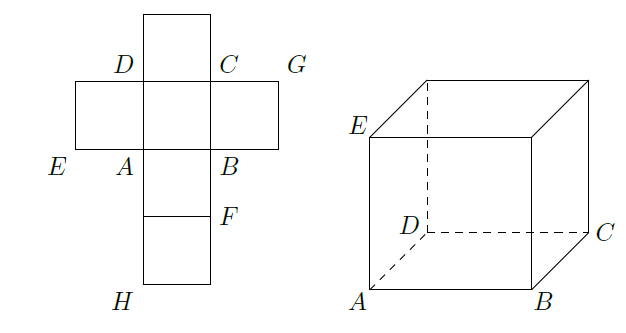
(Ⅰ)请按字母
标记在正方体相应地顶点处(不需要说明理由)
(Ⅱ)判断平面
与平面
的位置关系,并说明你的结论.
(Ⅲ)证明:直线
平面
.
如图  ,在直角梯形
中,
,
,
,
,
,在直角梯形
中,
,
,
,
,  是
的中点,
是
与
的交点.将
沿
折起到
的位置,如图
是
的中点,
是
与
的交点.将
沿
折起到
的位置,如图  .
.

(Ⅰ)证明:
平面
;
(Ⅱ)若平面
平面
,求平面
与平面
夹角的余弦值.
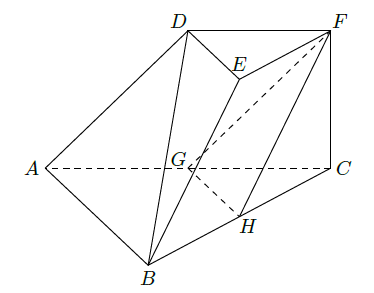
如图,三棱台DEF-ABC中,
分别为
的中点.
(Ⅰ)求证:
平面
;
(Ⅱ)若
求证:平面
平面
.
如图,在三棱台
中,
分别为
的中点.

(Ⅰ)求证:
平面
;
(Ⅱ)若
平面
,
,
,求平面
与平面
所成的角(锐角)的大小.
如图,三角形
所在的平面与长方形
所在的平面垂直,
,
,
.

(1)证明:
平面
;
(2)证明:
;
(3)求点
到平面
的距离.
如图,已知 平面
平面
 ,
, 为等边三角形,
为等边三角形,
(1)若平面 平面
平面 ,求CD长度;
,求CD长度;
(2)求直线AB与平面ADE所成角的取值范围.
试题篮
()