(本小题满分14分)如图, 是边长为
是边长为 的等边三角形,
的等边三角形, 是等腰直角三角形,
是等腰直角三角形, ,平面
,平面
 平面
平面 ,且
,且 平面
平面 ,
, .
.
(1)证明: 平面
平面 ;
;
(2)证明:
 .
.
.(本小题满分14分)如图,已知三棱锥 的三条侧棱
的三条侧棱 ,
, ,
, 两两垂直,△
两两垂直,△ 为等边三角形,
为等边三角形,  为△
为△ 内部一点,点
内部一点,点 在
在 的延长线上,且
的延长线上,且 .
.
(1)证明: ;
;
(2)证明:平面 平面
平面 ;
;
(3)若 ,
, ,求二面角
,求二面角 的余弦值.
的余弦值.
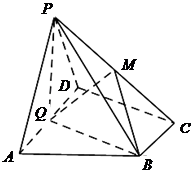
(本小题满分14分)如图,在四棱锥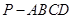 中,底面
中,底面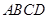 为直角梯形,
为直角梯形,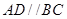 ,
,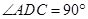 ,平面
,平面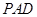 ⊥底面
⊥底面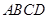 ,
,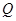 为
为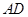 的中点,
的中点,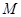 是棱
是棱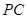 上的点,
上的点,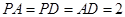 ,
,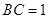 ,
,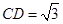 .
.
(1)求证:平面 ⊥平面
⊥平面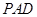 ;
;
(2)若二面角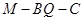 为
为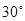 ,设
,设 ,试确定
,试确定 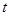 的值.
的值.
(本小题满分12分)如图,在菱形 中,
中, ,
, ,
,  分别是边
分别是边 ,
, 的中点,
的中点, ,沿
,沿 将△
将△ 翻折到△
翻折到△ ,连接
,连接 ,得到如图的五棱锥
,得到如图的五棱锥 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若 ,求二面角
,求二面角 的大小.
的大小.
如图所示,在三棱锥 中,
中, ,平面
,平面 ⊥平面
⊥平面 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
如图所示,在三棱锥 中,
中, ,平面
,平面 ⊥平面
⊥平面 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
如图,在三棱锥 中,
中, 平面
平面 ,
, ,
, ,
, 、
、 、
、 分别为
分别为 、
、 、
、 的中点,
的中点, 、
、 分别为线段
分别为线段 、
、 上的动点,且有
上的动点,且有 .
.
(1)求证: 面
面 ;
;
(2)探究:是否存在这样的动点M,使得二面角 为直二面角?若存在,求CM的长度;若不存在,说明理由.
为直二面角?若存在,求CM的长度;若不存在,说明理由.
如图,在三棱锥 中,
中, 平面
平面 ,
, ,
, ,
, 、
、 、
、 分别为
分别为 、
、 、
、 的中点,
的中点, 、
、 分别为线段
分别为线段 、
、 上的动点,且有
上的动点,且有 .
.
(1)求证: 面
面 ;
;
(2)探究:是否存在这样的动点M,使得二面角 为直二面角?若存在,求CM的长度;若不存在,说明理由.
为直二面角?若存在,求CM的长度;若不存在,说明理由.
试题篮
()