如图,已知椭圆的中心在坐标原点,焦点在 轴上,它的一个顶点为
轴上,它的一个顶点为 ,且离心率等于
,且离心率等于 ,过点
,过点 的直线
的直线 与椭圆相交于不同两点
与椭圆相交于不同两点 ,点
,点 在线段
在线段 上。
上。
(1)求椭圆的标准方程;
(2)设 ,若直线
,若直线 与
与 轴不重合,
轴不重合,
试求 的取值范围。
的取值范围。
如图,动点M与两定点A(-1,0),B(2,0)构成△MAB,且∠MBA=2∠MAB.设动点M的轨迹为C.
(1)求轨迹C的方程;
(2)设直线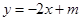 (其中
(其中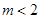 )与y轴相交于点P,与轨迹C相交于点Q,R,且
)与y轴相交于点P,与轨迹C相交于点Q,R,且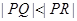 ,求
,求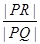 的取值范围.
的取值范围.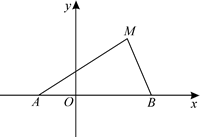
(本小题满分14分)已知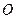 为坐标原点,点F、T、M、P分别满足
为坐标原点,点F、T、M、P分别满足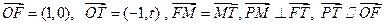 .
.
(1) 当t变化时,求点P的轨迹方程;
(2) 若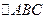 的顶点在点P的轨迹上,且点A的纵坐标
的顶点在点P的轨迹上,且点A的纵坐标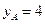 ,
,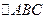 的重心恰好为点F,
的重心恰好为点F,
求直线BC的方程.
(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分.
已知两点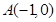 、
、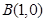 ,点
,点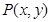 是直角坐标平面上的动点,若将点
是直角坐标平面上的动点,若将点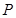 的横坐标保持不变、纵坐标扩大到
的横坐标保持不变、纵坐标扩大到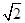 倍后得到点
倍后得到点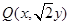 满足
满足 .
.
(1) 求动点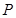 所在曲线
所在曲线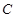 的轨迹方程;
的轨迹方程;
(2)(理科)过点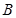 作斜率为
作斜率为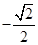 的直线
的直线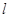 交曲线
交曲线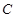 于
于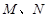 两点,且满足
两点,且满足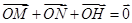 ,又点
,又点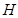 关于原点O的对称点为点
关于原点O的对称点为点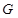 ,试问四点
,试问四点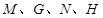 是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
(文科)过点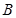 作斜率为
作斜率为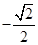 的直线
的直线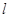 交曲线
交曲线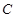 于
于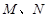 两点,且满足
两点,且满足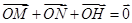 (O为坐标原点),试判断点
(O为坐标原点),试判断点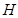 是否在曲线
是否在曲线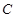 上,并说明理由.
上,并说明理由.
已知椭圆的离心率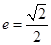 ,左、右焦点分别为
,左、右焦点分别为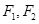 ,定点P
,定点P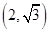 ,点
,点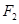 在线段
在线段 的中垂线上.
的中垂线上.
(1)求椭圆C的方程;
(2)设直线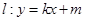 与椭圆C交于M、N两点,直线
与椭圆C交于M、N两点,直线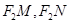 的倾斜角分别为
的倾斜角分别为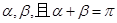 ,求证:直线
,求证:直线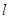 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
已知椭圆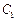 和抛物线
和抛物线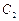 有公共焦点F(1,0),
有公共焦点F(1,0), 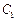 的中心和
的中心和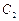 的顶点都在坐标原点,过点M(4,0)的直线
的顶点都在坐标原点,过点M(4,0)的直线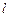 与抛物线
与抛物线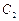 分别相交于A,B两点.
分别相交于A,B两点.
(Ⅰ)写出抛物线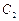 的标准方程;
的标准方程;
(Ⅱ)若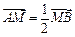 ,求直线
,求直线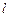 的方程;
的方程;
(Ⅲ)若坐标原点 关于直线
关于直线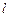 的对称点
的对称点 在抛物线
在抛物线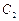 上,直线
上,直线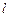 与椭圆
与椭圆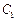 有公共点,求椭圆
有公共点,求椭圆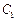 的长轴长的最小值.
的长轴长的最小值.
在平面直角坐标系中,两点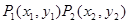 间的“L-距离”定义为
间的“L-距离”定义为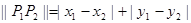 ,则平面内与
,则平面内与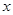 轴上两个不同的定点
轴上两个不同的定点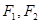 的“L-距离”之和等于定值(大于
的“L-距离”之和等于定值(大于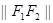 )的点的轨迹可以是( )
)的点的轨迹可以是( )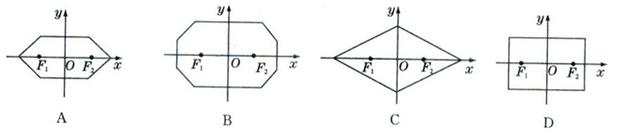
在平面直角坐标系中,两点间的"
距离"定义为
则平面内与
轴上两个不同的定点
的"
距离"之和等于定值(大于
)的点的轨迹可以是()
| A. |
|
B. |
|
| C. |
|
D. |
|
已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,两准线间的距离为4.
(Ⅰ)求椭圆的方程;
(Ⅱ)直线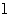 过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.
过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.
试题篮
()