建立适当的坐标系,用坐标法解决下列问题:
已知隧道的截面是半径为4m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7m,高为3m的货车能不能驶入这个隧道?
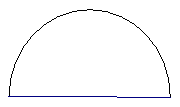 |
如图,在四边形ABCD中,AD=8,CD=6,AB=13,∠ADC=90°,且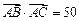 .
.
(1)求sin∠BAD的值;
(2)设△ABD的面积为S△ABD,△BCD的面积为S△BCD,求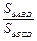 的值.
的值.
 |
在直角坐标系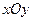 中,点
中,点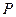 到两点
到两点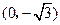 ,
,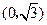 的距离之和等于
的距离之和等于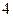 ,设点
,设点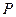 的轨迹为
的轨迹为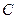 。
。
(1)求曲线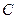 的方程;
的方程;
(2)过点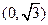 作两条互相垂直的直线
作两条互相垂直的直线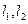 分别与曲线
分别与曲线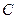 交于
交于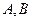 和
和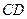 。
。
①以线段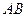 为直径的圆过能否过坐标原点,若能求出此时的
为直径的圆过能否过坐标原点,若能求出此时的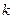 值,若不能说明理由;
值,若不能说明理由;
②求四边形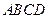 面积的取值范围。
面积的取值范围。
如图,圆 内有一点
内有一点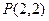 ,过点
,过点 作直线
作直线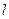 交圆于
交圆于 两点.(1)当直线
两点.(1)当直线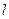 经过圆心
经过圆心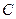 时,求直线
时,求直线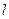 的方程;(2)当弦
的方程;(2)当弦 被点
被点 平分时,写出直线
平分时,写出直线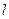 方程;(3)当直线
方程;(3)当直线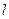 倾斜角为
倾斜角为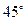 时,求
时,求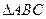 的面积.
的面积.

如下图所示,在直角坐标系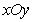 中,射线
中,射线 在第一象限,且与
在第一象限,且与 轴的正半轴成定角
轴的正半轴成定角 ,动点
,动点 在射线
在射线 上运动,动点
上运动,动点 在
在 轴的正半轴上运动,
轴的正半轴上运动, 的面积为
的面积为 .
.
(Ⅰ)求线段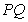 中点
中点 的轨迹
的轨迹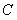 的方程;
的方程;
(Ⅱ) 是曲线
是曲线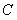 上的动点,
上的动点,  到
到 轴的距离之和为
轴的距离之和为 ,
,
设 为
为 到
到 轴的距离之积.问:是否存在最大的常数
轴的距离之积.问:是否存在最大的常数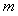 ,
,
使 恒成立?若存在,求出这个
恒成立?若存在,求出这个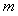 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知圆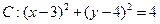 和直线
和直线 ,直线
,直线 ,
, 都经过圆C外
都经过圆C外
定点A(1,0).
(Ⅰ)若直线 与圆C相切,求直线
与圆C相切,求直线 的方程;
的方程;
(Ⅱ)若直线 与圆C相交于P,Q两点,与
与圆C相交于P,Q两点,与 交于N点,且线段PQ的中点为M,
交于N点,且线段PQ的中点为M,
求证: 为定值.
为定值.
已知半径为5的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
(1)求圆的方程;
(2)设直线 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数 ,使得过点
,使得过点 的直线
的直线 垂直平分弦
垂直平分弦 ?
?
存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
试题篮
()