设二次函数 在区间
在区间 上的最大值、最小值分别是
上的最大值、最小值分别是 ,集合
,集合 .
.
(Ⅰ)若 ,且
,且 ,求
,求 的值;
的值;
(Ⅱ)若 ,且
,且 ,记
,记 ,求
,求 的最小值.
的最小值.
已知中心在原点,焦点在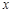 轴上的椭圆
轴上的椭圆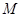 的离心率为
的离心率为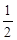 ,椭圆上异于长轴顶点的任意点
,椭圆上异于长轴顶点的任意点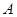 与左右两焦点
与左右两焦点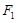 、
、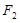 构成的三角形中面积的最大值为
构成的三角形中面积的最大值为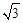 .
.
(1)求椭圆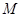 的标准方程;
的标准方程;
(2)已知点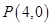 ,连接
,连接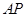 与椭圆的另一交点记为
与椭圆的另一交点记为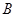 ,若
,若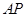 与椭圆相切时
与椭圆相切时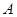 、
、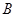 不重合,连接
不重合,连接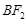 与椭圆的另一交点记为
与椭圆的另一交点记为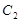 ,求
,求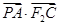 的取值范围.
的取值范围.
若f(x)的定义域为[a,b],值域为[a,b](a<b),则称函数f(x)是[a,b]上的“四维光军”函数.
①设g(x)= x2-x+
x2-x+ 是[1,b]上的“四维光军”函数,求常数b的值;
是[1,b]上的“四维光军”函数,求常数b的值;
②问是否存在常数a,b(a>-2),使函数h(x)= 是区间[a,b]上的“四维光军”函数?若存在,求出a,b的值,否则,请说明理由.
是区间[a,b]上的“四维光军”函数?若存在,求出a,b的值,否则,请说明理由.
设函数 ,其中
,其中 ,区间
,区间
(Ⅰ)求的长度(注:区间 的长度定义为
的长度定义为 );
);
(Ⅱ)给定常数 ,当时,求长度的最小值.
,当时,求长度的最小值.
函数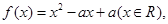 数列
数列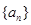 的前
的前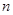 项和
项和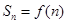 ,且
,且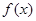 同时满足:①不等式
同时满足:①不等式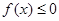 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在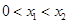 ,使得不等式
,使得不等式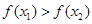 成立.
成立.
(1)求函数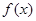 的表达式;
的表达式;
(2)求数列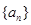 的通项公式.
的通项公式.
已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求a的取值范围
设二次函数 在区间
在区间 上的最大值、最小值分别是
上的最大值、最小值分别是 ,集合
,集合 .
.
(Ⅰ)若 ,且
,且 ,求
,求 的值;
的值;
(Ⅱ)若 ,且
,且 ,记
,记 ,求
,求 的最小值.
的最小值.
试题篮
()