 的内角
的内角 ,
, ,
, 的对边分别是
的对边分别是 ,
, ,
, ,若
,若 ,
, ,
, ,则
,则 = ( )
= ( )
A. |
B.2 | C. |
D.1 |
在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sin B(tan A+tan C)=tan Atan C.
(1)求证:a,b,c成等比数列;
(2)若a=1,c=2,求△ABC的面积S.
如图,为了测定河的宽度,在一岸边选定两点A,B和对岸标记物C,测得∠CAB=30°,∠CBA=45°,AB=120 m,则河的宽度为 m.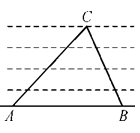
设△ABC的内角A, B, C所对的边分别为a, b, c, 若 , 则△ABC的形状为( )
, 则△ABC的形状为( )
| A.锐角三角形 | B.钝角三角形 | C.直角三角形 | D.不确定 |
如图,渔船甲位于岛屿 的南偏西
的南偏西 方向的
方向的 处,且与岛屿
处,且与岛屿 相距12海里,渔船乙以10海里/小时的速度从岛屿
相距12海里,渔船乙以10海里/小时的速度从岛屿 出发沿正北方向航行,若渔船甲同时从
出发沿正北方向航行,若渔船甲同时从 处出发沿北偏东
处出发沿北偏东 的方向追赶渔船乙,刚好用2小时追上.则
的方向追赶渔船乙,刚好用2小时追上.则 = .
= .
如图,在日本地震灾区的搜救现场,一条搜救狗从A处沿正北方向行进x m到达B处发现一个生命迹象,然后向右转105°,行进10 m到达C处发现另一生命迹象,这时它向右转135°后继续前行回到出发点,那么x=________.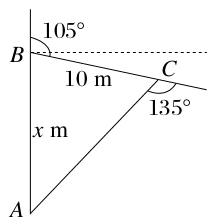
试题篮
()