高中数学表面展开图解答题

（本小题共14分）如图，在四棱锥S-ABCD中，底面ABCD为菱形，∠BAD=60^°，平面SAD⊥平面ABCD，SA=SD，E，P，Q分别是棱AD，SC，AB的中点．

（Ⅰ）求证：PQ∥平面SAD；
（Ⅱ）求证：AC⊥平面SEQ；
（Ⅲ）如果SA=AB=2，求三棱锥S-ABC的体积．

如图，设四棱锥的底面为菱形，且∠，，。

（1）求证：平面平面；
（2）设为的中点,求三棱锥的体积．

在长方体中，，分别是所在棱的中点，点是棱上的动点，联结．如图所示．

（1）求异面直线所成角的大小（用反三角函数值表示）；
（2）求以为顶点的三棱锥的体积．

（本小题满分12分）如图，已知⊙O的直径AB=3，点C为⊙O上异于A，B的一点，VC⊥平面ABC，且VC=2，点M为线段VB的中点.

（1）求证：BC⊥平面VAC；
（2）若直线AM与平面VAC所成角为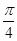.求三棱锥B-ACM的体积.

（本小题满分12分）如图，在四棱锥P－ABCD中，E为AD上一点，PE⊥平面ABCD，AD∥BC，AD⊥CD，BC＝ED＝2AE，F为PC上一点，且CF＝2FP.

（1）求证：PA∥平面BEF；
（2）求三棱锥P－ABF与三棱锥F－EBC的体积之比.

如图，在正三棱柱中， 点D为棱AB的中点，BC=1，.

（1）求证：∥平面；
（2）求三棱锥 的体积.

（本小题满分12分）如图,在棱长为2的正方体中，点E，F分别是棱AB，BC上的动点，且AE=BF．

（Ⅰ）求证：A₁FC₁E；
（Ⅱ）当三棱锥的体积取得最大值时，求二面角的正切值．

（本小题7分）.如图，在四棱锥中，底面是正方形，侧棱，，是的中点，交于点．

（1）证明 //平面；
（2）证明⊥平面；
（3）求.

如图，储油灌的表面积为定值，它的上部是半球，下部是圆柱，半球的半径等于圆柱底面半径．

（1）试用半径表示出储油灌的容积，并写出的范围．
（2）当圆柱高与半径的比为多少时，储油灌的容积最大？

五边形是由一个梯形与一个矩形组成的，如图甲所示，为的中点，.现沿着虚线将五边形折成直二面角，如图乙所示．

（1）求证：平面平面；
（2）求图乙中的多面体的体积.

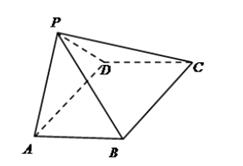
（本小题满分12分）如图，四棱锥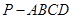中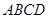，为矩形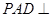，平面平面．

（Ⅰ）求证：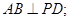
（Ⅱ）若，问当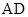为何值时，四棱锥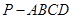的体积最大？并求其最大体积.

将12cm长的细铁线截成三条长度分别为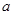、、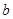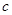的线段，
（1）求以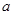、、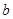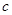为长、宽、高的长方体的体积的最大值；
（2）若这三条线段分别围成三个正三角形，求这三个正三角形面积和的最小值。

（本小题满分14分）四棱锥 中，底面是正方形，，垂足为点，，点分别是的中点．

（1）求证：；
（2）求证：；
（3）求四面体的体积．

（本小题满分14分）如图所示,平面平面,且四边形为正方形,,∥,,为的中点．

（1）求证：∥平面；
（2）求证：平面;
（3）求三棱锥的体积.

（本小题满分14分）在棱长为2的正方体中，设是棱的中点。

（1）求证：；
（2）求证：平面；
（3）求三棱锥的体积.