高中数学表面展开图解答题

（本小题满分12分）已知三棱锥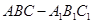中，侧棱垂直于底面，点是的中点．

（1）求证：平面；
（2）若底面为边长为的正三角形，，求三棱锥的体积．

（本小题满分12分）如图，四棱锥中，是正三角形，四边形是矩形，且平面平面，，．

（Ⅰ）若点是的中点，求证：平面；
（Ⅱ）若点在线段上，且，当三棱锥的体积为时，求实数的值．

（本小题满分12分）如图，在斜三棱柱中，侧面与侧面都是菱形，，．

（Ⅰ）求证：；
（Ⅱ）若，求四棱锥的体积．

（本小题满分12分）如图是图的三视图，三棱锥中，，分别是棱，的中点．

（1）求证：平面；
（2）求三棱锥的体积．

（本小题满分12分）如图，设四棱锥的底面为菱形，且，，．

（1）证明：平面平面；
（2）求四棱锥的体积．

【改编】如图，在直三棱柱中，D、E分别为、AD的中点，F为上的点，且

（Ⅰ）证明：EF∥平面ABC；
（Ⅱ）若，，
（Ⅰ）求三棱锥的体积；
（Ⅱ）求二面角的大小．

（本小题满分14分）某商场为促销要准备一些正三棱锥形状的装饰品，用半径为的圆形包装纸包装．要求如下：正三棱锥的底面中心与包装纸的圆心重合，包装纸不能裁剪，沿底边向上翻折，其边缘恰好达到三棱锥的顶点，如图所示．设正三棱锥的底面边长为，体积为．

（1）求关于的函数关系式；
（2）在所有能用这种包装纸包装的正三棱锥装饰品中，的最大值是多少？并求此时的值．

（本小题满分12分）如图所示，直角梯形与等腰直角所在平面互相垂直，为的中点，，∥，．

（Ⅰ）求证：平面平面；
（Ⅱ）求证：∥平面；
（Ⅲ）求四面体的体积．

（本小题满分12分）如图，在四棱锥中，底面是菱形，，平面，，点，分别为为和中点．

（1）求证：直线平面；
（2）求三棱锥的表面积．

（本小题满分14分） 如图，矩形中，，．，分别在线段和上，∥，将矩形沿折起．记折起后的矩形为，且平面平面．

（Ⅰ）求证：∥平面；
（Ⅱ）若，求证：；
（Ⅲ）求四面体体积的最大值．

（本小题满分12分）如图，三棱柱ABC－A₁B₁C₁中，平面ABB₁A₁⊥底面ABC，，∠A₁AB＝120°，D、E分别是BC、A₁C₁的中点．

（Ⅰ）试在棱AB上找一点F，使DE∥平面A₁CF；
（Ⅱ）在（Ⅰ）的条件下，求多面体BCF－A₁B₁C₁的体积．

（本小题满分14分）如图，直角梯形，，，，点为的中点，将沿折起，使折起后的平面与平面垂直（如图）．在下图所示的几何体中：

（1）求证：平面；
（2）点在棱上，且满足平面，求几何体的体积．

（本小题满分12分）如图，在多面体ABCDEF中，ABCD是边长为2的正方形，是一平行四边形，且DE平面ABCD，BF=3，G和H分别是CE和CF的中点。

（Ⅰ）求证：平面AEF//平面BDGH；
（Ⅱ）求

（本小题满分12分）为等腰直角三角形，，，、分别是边和的中点，现将沿折起，使面面，是边的中  
点，平面与交于点．

（Ⅰ）求证：；
（Ⅱ）求三棱锥的体积.

（本小题满分12分）如图，已知在直三棱柱中, ，，点D是线段的中点．

（Ⅰ）求证：∥平面；
（Ⅱ）当三棱柱的体积最大时，求直线与平面所成角的正弦值．