(本小题满分14分)
如图,四棱锥 的底面
的底面 是边长为
是边长为 的正方形,
的正方形, 平面
平面 ,点
,点 是
是 的中点.
的中点.
⑴求证: 平面
平面 ;
;
⑵求证:平面 平面
平面 ;
;
⑶若 ,求三棱锥
,求三棱锥 的体积.
的体积.
(本小题满分12分)
在边长为 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).

(Ⅰ)在三棱锥上标注出 、
、 点,并判别MN与平面AEF的位置关系,并给出证明;
点,并判别MN与平面AEF的位置关系,并给出证明;
(Ⅱ) 是线段
是线段 上一点,且
上一点,且 , 问是否存在点
, 问是否存在点 使得
使得 ,若存在,求出
,若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)求多面体E-AFNM的体积.
(本小题共14分)
如图所示多面体中,AD⊥平面PDC,ABCD为平行四边形,E,F分别为AD,BP的中点,AD= ,AP=
,AP= ,PC=
,PC= .
.
(Ⅰ)求证:EF∥平面PDC;
(Ⅱ)若∠CDP=90°,求证BE⊥DP;
(Ⅲ)若∠CDP=120°,求该多面体的体积.
(本小题满分14分)
在一个半径为1的半球材料中截取三个高度均为h的圆柱,其轴截面如图所示,设三个圆柱体积之和为 。
。
(1) 求f(h)的表达式,并写出h的取值范围是 ;
(2) 求三个圆柱体积之和V的最大值;
如图分别是正三棱台ABC-A1B1C1的直观图和正视图,O,O1分别是上下底面的中心,E是BC中点.
(1)求正三棱台ABC-A1B1C1的体积;
(2)求平面EA1B1与平面A1B1C1的夹角的余弦;
(3)若P是棱A1C1上一点,求CP+PB1的最小值.
如图,已知 是底面边长为1的正四棱柱,
是底面边长为1的正四棱柱,
(1)证明:平面 平面
平面
(2)当二面角 的平面角为120°时,求四棱锥
的平面角为120°时,求四棱锥 的体积。
的体积。
如图,多面体ABCDS中,面ABCD为矩形, 且
且 ,
,
 。(I)求多面体ABCDS的体积;(II)求AD与SB所成角的余弦值;(III)求二面角A—SB—D的余弦值。
。(I)求多面体ABCDS的体积;(II)求AD与SB所成角的余弦值;(III)求二面角A—SB—D的余弦值。
如图,已知圆锥体 的侧面积为
的侧面积为 ,底面半径
,底面半径 和
和 互相垂直,且
互相垂直,且 ,
, 是母线
是母线 的中点.
的中点.
(1)求圆锥体的体积;
(2)异面直线 与
与 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
(本小题满分12分) 如图所示,等腰△ABC的底边AB= ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积.
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积.
(Ⅰ)求V(x)的表达式;
(Ⅱ)当x为何值时,V(x)取得最大值?
(本小题满分12分)如图,已知矩形 所在平面与矩形
所在平面与矩形 所在平面垂直,
所在平面垂直, ,
, =1,
=1, ,
, 是线段
是线段 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求多面体 的表面积;
的表面积;
(3)求多面体 的体积.
的体积.
如图,在四面体 中,平面
中,平面 平面
平面 ,
, ,
, ,
, 。
。
(Ⅰ)若 ,
,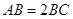 ,求四面体
,求四面体 的体积;
的体积;
(Ⅱ)若二面角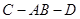 为
为 ,求异面直线
,求异面直线 与
与 所成角的余弦值。
所成角的余弦值。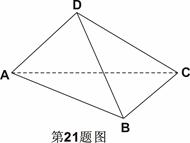
试题篮
()