圆 外一点
外一点 向这个圆作两条切线,则两切线夹角的余弦值为( )
向这个圆作两条切线,则两切线夹角的余弦值为( )
A. |
B. |
C. |
D. |
圆 的切线方程中有一个是 ( )
的切线方程中有一个是 ( )
| A.x-y=0 | B.x+y=0 | C.x=0 | D.y=0 |
设椭圆的两个焦点分别为 ,过
,过 作椭圆长轴的垂线交椭圆于点P,若△
作椭圆长轴的垂线交椭圆于点P,若△
为等腰直角三角形,则椭圆的离心率为( )
A. B.
B. C
C .
. D.
D.
已知 是椭圆的两个焦点,过
是椭圆的两个焦点,过 且与椭圆长轴垂直的直线交椭圆于A、B两点,
且与椭圆长轴垂直的直线交椭圆于A、B两点,
若△ 是正三角形,则这个椭圆的离心率为( )
是正三角形,则这个椭圆的离心率为( )
A. B.
B. C.
C. D.
D.
已知定点A、B,且|AB|=4,动点P满足|PA|-|PB|=3,则|PA|的最小值是( )
A.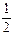 B.
B.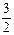 C.
C.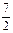 D.5
D.5
对于抛物线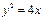 上任意一点Q,点
上任意一点Q,点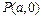 都满足
都满足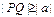 .则
.则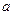 的取值范围是( )
的取值范围是( )
A.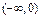 |
B.(-∞,2) | C.[0,2] | D.(0,2) |
(本小题满分12分)点P到M(-1,0)、N(1,0)的距离之差为2m,到x轴、y轴的距离之比为2.求m的取值范围.
(本小题满分12分)点A、B分别是椭圆 长轴的左、右端点,点F是
长轴的左、右端点,点F是
椭圆的右焦点,点P在椭圆上,且位于 轴上方,
轴上方, .
.
(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线A P的距离等于
P的距离等于 ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离 的最小值.
的最小值.
(本小题满分12分)
设 ,
,
 两点在抛物线
两点在抛物线 上,
上, 是
是 的垂直平分线.
的垂直平分线.
( 1)当且仅当
1)当且仅当 取何值时,直线
取何值时,直线 经过抛物线的焦点
经过抛物线的焦点 ?证明你的结论;
?证明你的结论;
(2)当直线 的斜率为2时,求
的斜率为2时,求 在
在 轴上截距的取值范围.
轴上截距的取值范围.
(本小题满分12分)在平面直角坐标系xOy中,有一个以为 和
和 焦点、离心率为
焦点、离心率为 的椭圆.设椭圆在第一象限的部分为曲线C, 动点P在C上, C在点P处
的椭圆.设椭圆在第一象限的部分为曲线C, 动点P在C上, C在点P处
的切线与x , y轴的交点分别为A、B,且向量 .求:
.求:
(1)点M的轨迹方程;
(2) 的最小值.
的最小值.
(本小题满分12分)
P、Q、M、N四点都在椭圆 上,F为椭圆在y轴正半轴上的焦点.已知
上,F为椭圆在y轴正半轴上的焦点.已知 与
与 共
共
线,且 与
与 共线.求四边形PMQN的面积的最小值和最大值.
共线.求四边形PMQN的面积的最小值和最大值.
试题篮
()