初中数学幂的乘方与积的乘方解答题

若、互为相反数，、互为倒数，的绝对值等于2，计算的值。

腾冲红叶公司去年1～3月平均每月亏损15万元,4～6月平均每月盈利20万元,7～10月平均每月盈利17万元,11～12月平均每月亏损23万元.这个公司去年总的盈利如何?

一只小虫从某点P出发，在一条直线上来回爬行，假定把向右爬行的路程记为正数，向左爬行的路程记为负数，则爬行各段路程（单位：厘米）依次为：+5，-3，+10，-8，-6，+12，-10。
（1）通过计算说明小虫是否能回到起点P。
（2）如果小虫爬行的速度为0.5厘米/秒，那么小虫共爬行了多长时间？

（每小题4分，共24分）
（1）－15－（－8）+（－11）－12           
（2）（－）×（）×÷（－）
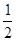（3）（－2）²+4×（－3）²－（－4）²÷（－2）  
（4）－5m²n+4mn²－2mn+6m²n+3mn
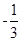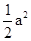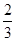（5）ab－+－（－ab）      
（6）4x²－[x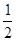－（x－3）+3x²]

已知某粮库已存有粮食100吨，本周内粮库进出粮食的记录如下（运进为正）：

星期	一	二	三	四	五	六	日
进、出记录	+35	－20	－30	+25	－24	+50	－26

 
（1）通过计算，说明本周内哪天粮库剩下的粮食最多？
（2）若运进的粮食为购进的，购买价格为每吨2000元，进出的粮食为卖出的价格为每吨2300元，则这一周的利润为多少？
（3）若每周平均进出的粮食大致相同，则再过几周粮库存的粮食可达到200吨？

（本题10分）已知数轴上点A与点B的距离为16个单位长度，点A在原点的左侧，到原点的距离为26个单位长度，点B在点A的右侧，点C表示的数与点B表示的数互为相反数，动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．
（1）点A表示的数为     ，点B表示的数为      ，点C表示的数为     ．
（2）用含t的代数式表示P到点A和点C的距离： PA=           ，PC=           ．
（3）当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回，运动到终点A．①在点Q向点C运动过程中，能否追上点P?若能，请求出点Q运动几秒追上．②在点Q开始运动后，P、Q两点之间的距离能否为2个单位？如果能，请求出此时点P表示的数；如果不能，请说明理由．

计算或化简：（每题3分）
①8＋(－10)―(―5)     
②  
③
④(5x－3y)－(2x－y)
⑤a²－a－[2a－(3a²＋a)]

（本题6分）我们把分子为1的分数叫做单位分数. 如，，，任何一个单位分数都可以拆分成两个不同的单位分数的和，如＝，＝，＝，
（1）根据对上述式子的观察，你会发现＝. 请写出□，○所表示的数；
（2）思考，单位分数（n是不小于2的正整数）＝，请写出△，☆所表示的式。
（3）计算：

（本题5分）某自行车厂一周计划生产1050辆自行车，平均每天生产150辆，由于各种原因实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产为正、减产为负）：

星期	一	二	三	四	五	六	日
增减	+5	-2	-4	+13	-10	+16	-9

 
（1）产量最多的一天比产量最少的一天多生产     辆；
（2）根据记录可知前三天共生产     辆；
（3）该厂实行计件工资制，每辆车50元，超额完成任务每辆奖10元，少生产一辆扣10元，那么该厂工人这一周的工资总额是多少？

某型号汽车油箱的最大贮油量为60L，在正常情况下，每行驶50km耗油5.5L．
（1）在加满油的情况下，该车正常行驶x km后，油箱内还剩的油量是多少？
（2）试通过计算判断，在加满油的情况下，若该车要正常行驶到550km外的某地，中途是否需要再加油？

邮递员骑车从邮局出发，先向西骑行3km到达A村，继续向西骑行２km到达B村，然后向东骑行7km到达C村，再继续向东骑行3km到达D村，最后骑回邮局．
（1）C村离A村有多远？
（2）邮递员一共骑行了多少千米？

在数轴上把下列各数表示出来，并用“<”连接各数，
，1，0，，－（＋1），4

观察下列等式：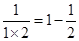
，，，
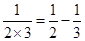将以上三个等式两边分别相加得：
．
（1）猜想并写出： 
（2）直接写出下列各式的计算结果：
        _____
（3）探究并利用以上规律计算：

用数轴上的点表示下列各有理数：， 2.5，， +5，并把它们按从大到小的顺序用＞号连接起来.

已知点A在数轴上对应的数是a，点B在数轴上对应的数是b，且．
现将A、B之间的距离记作，定义．
（1）的值
（2）的值
（3）设点P在数轴上对应的数是x，当时，求x的值；