初中数学幂的乘方与积的乘方解答题

（本题5分）若新规定这样一种运算法则：a※b=a²+2ab， 
例如3※（-2）=3²+2×3×（-2）=－3
（1）试求（－2）※3的值
（2）若（－2）※x=－2+ x , 求x的值

（每小题4分，共16分）计算：
（1），      
（2），
（3）           
（4）

先在数轴上画出表示下列各数的点，然后将这些数用“＜”号连接起来.
－2²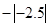，，(－1)²⁰¹⁴，π

（本题共10分）如图，点P、Q在数轴上表示的数分别是－8、4，点P以每秒2个单位的速度
运动，点Q以每秒1个单位的速度运动．设点P、Q同时出发，运动时间为t秒．

（1）若点P、Q同时向右运动2秒，则点P表示的数为_______，点P、Q之间的距离是______个单位；
（2）经过__________秒后，点P、Q重合；
（3）试探究：经过多少秒后，点P、Q两点间的距离为14个单位．

（本题共6分）观察下列各式的计算结果：
1－＝1－＝＝×          1－＝1－＝＝×
1－＝1－＝＝×       1－＝1－＝＝× ……
（1）用你发现的规律填写下列式子的结果：
1－＝     ×     ；          1－＝      ×      ；
（2）用你发现的规律计算：
（1－）×（1－）×（1－）×…×（1－）×（1－）．

有8筐白菜，以每筐25千克为标准，超过的千克数记作正数，不足的千克数记作负数，称后
的纪录如下：回答下列问题：

（1）这8筐白菜中最接近标准重量的这筐白菜重     千克；
（2）若这批白菜以2元 ∕ 千克的价格出售，则这批白菜一共可获利多少元？

（本题14分）已知数轴上有A，B，C三点，分别代表－24，－10，10，两只电子蚂蚁甲，乙分别从A，C两点同时相向而行，甲的速度为4个单位／秒．
（1）问多少秒后，甲到A，B，C的距离和为40个单位？
（2）若乙的速度为6个单位／秒，两只电子蚂蚁甲，乙分别从A，C两点同时相向而行，问甲，乙在数轴上的哪个点相遇？
（3）在（1）（2）的条件下，当甲到A、B、C的距离和为40个单位时，甲调头返回．问甲，乙还能在数轴上相遇吗？若能，求出相遇点；若不能，请说明理由．

（本题12分）某自行车厂一周计划生产1400辆自行车，平均每天生产200辆，由于各种原因实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产为正、减产为负）：

星期	一	二	三	四	五	六	日
增减	＋5	－2	－4	＋13	－10	＋16	－9

 
（1）根据记录可知前三天共生产 辆；
（2）产量最多的一天比产量最少的一天多生产 辆；
（3）该厂实行每周计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣15元，那么该厂工人这一周的工资总额是多少？

（本题6分）a，b为有理数，如果规定一种新的运算“”，定义：ab＝a²－ab＋a－1，请根据“”的定义计算下列各题：
例如：2（－5）＝
＝4－（－10）＋2－1＝4＋10＋2－1＝15
计算：（13）（－3）

一名足球守门员练习折返跑，从球门线出发，向前记作正数，返回记作负数，他的记录如下：（单位：米）+5，-3，+10，-8，-6，+12，-10
（1）守门员最后是否回到了球门线的位置？
（2）在练习过程中，守门员离开球门最远距离是多少米？
（3）守门员全部练习结束后，他共跑了多少米？

“埃博拉”病毒是一种能引起人类和灵长类动物产生“出血热”的烈性传染病毒，传染性极强.一日本人在非洲旅游时不慎感染了“埃博拉”病毒，经过两轮传染后，共有64人受到感染.
（1）问每轮传染中平均一个人传染了几个人？
（2）如果不及时控制，第三轮将又有多少人被传染？

（本题10分）（1）观察一列数，，，，…，发现从第二项开始，每一项与前一项之比是一个常数，这个常数是_______；根据此规律，如果a_n（n为正整数）表示这个数列的第n项，那么＝_______，＝_______；（可用幂的形式表示）
（2）如果想要求的值，可令①
将①式两边同乘以2，得___________              ②，
由②减去①式，得＝__________________．
（3）若（1）中数列共有20项，设，请利用上述规律和方法计算的值．（列式计算）

（本题8分）阅读下列材料：计算.
解法一：原式=．
解法二：原式=．
解法三：原式的倒数为.
故原式=300．
上述得出的结果不同，肯定有错误的解法，你认为解法           是错误的．请你选择合适的解法解答下列问题：计算：

（本题8分）某工艺厂计划一周生产工艺品280个，平均每天生产40个，但实际每天生产量与计划相比有出入．下表是某周的生产情况（以40个为标准，超产记为正、减产记为负）：

（1）根据记录的数据，该厂星期一生产工艺品的数量为多少个？（列式计算）
（2）根据记录的数据，该厂本周产量最多的一天比最少的一天多生产           多少个工艺品？（列式计算）
（3）该工艺厂在本周实际生产工艺品的数量为多少个？（列式计算）
（4）已知该厂实行每周计件工资制，每周结算一次，每生产一个工艺品可得10元，若超额完成任务（以280个为标准），则超过部分每个另奖20元，少生产一个扣10元．试求该工艺厂在这一周应付出的工资总额．

“十•一”黄金周期间，某公园在7天假期中每天旅游的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）

日期	1日	2日	3日	4日	5日	6日	7日
人数变化（万人）	+1.6	+0.8	+0.4	-0.4	-0.8	+0.2	-1.2

 
（1）若9月30日的游客人数记为a，请用a的代数式表示10月2日的游客人数？
（2）请判断七天内游客人数最多的是哪天？请说明理由；
（3）若9月30日的游客人数为2万人，门票每人80元．问黄金周期间该公园门票收入是多少元？（用科学记数法表示）