初中数学二次函数的应用解答题

2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年，荆门市政府加大各部门和单位对口扶贫力度．某单位的帮扶对象种植的农产品在某月（按30天计）的第 $x$ 天 $(x$ 为正整数）的销售价格 $p$ （元 $/$ 千克）关于 $x$ 的函数关系式为 $p=\left\{\begin{array}{c}\frac{2}{5}x+4(0<x⩽20)\\ -\frac{1}{5}x+12(20<x⩽30)\end{array}\right.$ ，销售量 $y$ （千克）与 $x$ 之间的关系如图所示．

（1）求 $y$ 与 $x$ 之间的函数关系式，并写出 $x$ 的取值范围；

（2）当月第几天，该农产品的销售额最大，最大销售额是多少？（销售额 $=$ 销售量 $\times$ 销售价格）

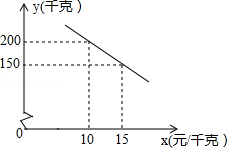
某药店选购了一批消毒液，进价为每瓶10元，在销售过程中发现，每天销售量 $y$（瓶 $)$与每瓶售价 $x$（元 $)$之间存在一次函数关系（其中 $10⩽x⩽21$，且 $x$为整数）．当每瓶消毒液售价为12元时，每天销售量为90瓶；当每瓶消毒液售价为15元时，每天销售量为75瓶．

（1）求 $y$与 $x$之间的函数关系式；

（2）设该药店销售该消毒液每天的销售利润为 $w$元，当每瓶消毒液售价为多少元时，药店销售该消毒液每天销售利润最大，最大利润是多少元？

黔东南州某超市购进甲、乙两种商品，已知购进3件甲商品和2件乙商品，需60元；购进2件甲商品和3件乙商品，需65元．

（1）甲、乙两种商品的进货单价分别是多少？

（2）设甲商品的销售单价为（单位：元件），在销售过程中发现：当时，甲商品的日销售量（单位：件）与销售单价之间存在一次函数关系，、之间的部分数值对应关系如表：

销售单价（元件）	11	19
日销售量（件	18	2

请写出当时，与之间的函数关系式．

（3）在（2）的条件下，设甲商品的日销售利润为元，当甲商品的销售单价（元件）定为多少时，日销售利润最大？最大利润是多少？

某网店销售一种儿童玩具，进价为每件30元，物价部门规定每件儿童玩具的销售利润不高于进价的 $60\%$．在销售过程中发现，这种儿童玩具每天的销售量 $y$（件 $)$与销售单价 $x$（元 $)$满足一次函数关系．当销售单价为35元时，每天的销售量为350件；当销售单价为40元时，每天的销售量为300件．

（1）求 $y$与 $x$之间的函数关系式．

（2）当销售单价为多少时，该网店销售这种儿童玩具每天获得的利润最大，最大利润是多少？

某工厂用50天时间生产一款新型节能产品，每天生产的该产品被某网店以每件80元的价格全部订购，在生产过程中，由于技术的不断更新，该产品第天的生产成本（元件）与（天之间的关系如图所示，第天该产品的生产量（件与（天满足关系式．

（1）第40天，该厂生产该产品的利润是　　元；

（2）设第天该厂生产该产品的利润为元．

①求与之间的函数关系式，并指出第几天的利润最大，最大利润是多少？

②在生产该产品的过程中，当天利润不低于2400元的共有多少天？

某商品的进价为每件40元，在销售过程中发现，每周的销售量 $y$（件 $)$与销售单价 $x$（元 $)$之间的关系可以近似看作一次函数 $y=\mathit{kx}+b$，且当售价定为50元 $/$件时，每周销售30件，当售价定为70元 $/$件时，每周销售10件．

（1）求 $k$， $b$的值；

（2）求销售该商品每周的利润 $w$（元 $)$与销售单价 $x$（元 $)$之间的函数解析式，并求出销售该商品每周可获得的最大利润．

某商店销售一种商品，经市场调查发现：该商品的周销售量（件是售价（元件）的一次函数，其售价、周销售量、周销售利润（元的三组对应值如表：

售价（元件）	50	60	80
周销售量（件	100	80	40
周销售利润（元	1000	1600	1600

注：周销售利润周销售量（售价进价）

（1）①求关于的函数解析式（不要求写出自变量的取值范围）；

②该商品进价是　　元件；当售价是　　元件时，周销售利润最大，最大利润是　　元．

（2）由于某种原因，该商品进价提高了元件，物价部门规定该商品售价不得超过65元件，该商店在今后的销售中，周销售量与售价仍然满足（1）中的函数关系．若周销售最大利润是1400元，求的值．

网络销售是一种重要的销售方式．某乡镇农贸公司新开设了一家网店，销售当地农产品．其中一种当地特产在网上试销售，其成本为每千克10元．公司在试销售期间，调查发现，每天销售量 $y\left(\mathit{kg}\right)$与销售单价 $x$（元 $)$满足如图所示的函数关系（其中 $10<x⩽30)$．

（1）直接写出 $y$与 $x$之间的函数关系式及自变量的取值范围．

（2）若农贸公司每天销售该特产的利润要达到3100元，则销售单价 $x$应定为多少元？

（3）设每天销售该特产的利润为 $W$元，若 $14<x⩽30$，求：销售单价 $x$为多少元时，每天的销售利润最大？最大利润是多少元？

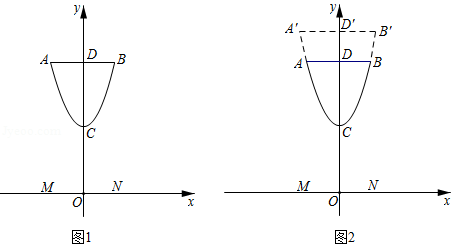
小聪设计奖杯，从抛物线形状上获得灵感，在平面直角坐标系中画出截面示意图，如图1，杯体 $\mathit{ACB}$ 是抛物线的一部分，抛物线的顶点 $C$ 在 $y$ 轴上，杯口直径 $\mathit{AB}=4$ ，且点 $A$ ， $B$ 关于 $y$ 轴对称，杯脚高 $\mathit{CO}=4$ ，杯高 $\mathit{DO}=8$ ，杯底 $\mathit{MN}$ 在 $x$ 轴上．

（1）求杯体 $\mathit{ACB}$ 所在抛物线的函数表达式（不必写出 $x$ 的取值范围）；

（2）为使奖杯更加美观，小敏提出了改进方案，如图2，杯体 $A\text{'}\mathit{CB}\text{'}$ 所在抛物线形状不变，杯口直径 $A\text{'}B\text{'}//\mathit{AB}$ ，杯脚高 $\mathit{CO}$ 不变，杯深 $\mathit{CD}\text{'}$ 与杯高 $\mathit{OD}\text{'}$ 之比为0.6，求 $A\text{'}B\text{'}$ 的长．

今年以来，我市接待的游客人数逐月增加，据统计，游玩某景区的游客人数三月份为4万人，五月份为5.76万人．

（1）求四月和五月这两个月中该景区游客人数平均每月增长百分之几；

（2）若该景区仅有 $A$ ， $B$ 两个景点，售票处出示的三种购票方式如下表所示：

购票方式	甲	乙	丙
可游玩景点	$A$	$B$	$A$ 和     $B$
门票价格	100元     $/$ 人	80元     $/$ 人	160元     $/$ 人

据预测，六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万，并且当甲、乙两种门票价格不变时，丙种门票价格每下降1元，将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票．

①若丙种门票价格下降10元，求景区六月份的门票总收入；

②问：将丙种门票价格下降多少元时，景区六月份的门票总收入有最大值？最大值是多少万元？

某商场购进甲、乙两种商品共100箱，全部售完后，甲商品共盈利900元，乙商品共盈利400元，甲商品比乙商品每箱多盈利5元．

（1）求甲、乙两种商品每箱各盈利多少元？

（2）甲、乙两种商品全部售完后，该商场又购进一批甲商品，在原每箱盈利不变的前提下，平均每天可卖出100箱．如调整价格，每降价1元，平均每天可多卖出20箱，那么当降价多少元时，该商场利润最大？最大利润是多少？

某乡镇实施产业扶贫，帮助贫困户承包了荒山种植某品种蜜柚，到了收获季节，已知该蜜柚的成本价为8元 $/$千克，投入市场销售时，调查市场行情，发现该蜜柚销售不会亏本，且每天销售量 $y$（千克）与销售单价 $x$（元 $/$千克）之间的函数关系如图所示．

（1）求 $y$与 $x$的函数关系式，并写出 $x$的取值范围；

（2）当该品种的蜜柚定价为多少时，每天销售获得的利润最大？最大利润是多少？

（3）某农户今年共采摘蜜柚4800千克，该品种蜜柚的保质期为40天，根据（2）中获得最大利润的方式进行销售，能否销售完这批蜜柚？请说明理由．

结合西昌市创建文明城市要求，某小区业主委员会决定把一块长 $80m$，宽 $60m$的矩形空地建成花园小广场，设计方案如图所示，阴影区域为绿化区（四块绿化区为全等的直角三角形），空白区域为活动区，且四周出口宽度一样，其宽度不小于 $36m$，不大于 $44m$，预计活动区造价60元 $/m^2$，绿化区造价50元 $/m^2$，设绿化区域较长直角边为 $\mathit{xm}$．

（1）用含 $x$的代数式表示出口的宽度；

（2）求工程总造价 $y$与 $x$的函数关系式，并直接写出 $x$的取值范围；

（3）如果业主委员会投资28.4万元，能否完成全部工程？若能，请写出 $x$为整数的所有工程方案；若不能，请说明理由．

（4）业主委员会决定在（3）设计的方案中，按最省钱的一种方案，先对四个绿化区域进行绿化，在实际施工中，每天比原计划多绿化 $11m^2$，结果提前4天完成四个区域的绿化任务，问原计划每天绿化多少 $m^2$．

某公司研发了一款成本为60元的保温饭盒，投放市场进行试销售，按物价部门规定，其销售单价不低于成本，但销售利润不高于 $65\%$，市场调研发现，保温饭盒每天的销售数量 $y$（个 $)$与销售单价 $x$（元 $)$满足一次函数关系；当销售单价为70元时，销售数量为160个；当销售单价为80元时，销售数量为140个（利润率 $=\frac{\mathit{利润}}{\mathit{成本}}\times 100\backslash \%)$

（1）求 $y$与 $x$之间的函数关系式；

（2）当销售单价定为多少元时，公司每天获得利润最大，最大利润为多少元？

某公司计划从甲、乙两种产品中选择一种生产并销售，每年产销x件．已知产销两种产品的有关信息如表：

产品	每件售价（万元）	每件成本（万元）	每年其他费用（万元）	每年最大产销量（件）
甲	6	a	20	200
乙	20	10	40+0.05x^2	80

其中a为常数，且 $3\le a\le 5$。

（1）若产销甲、乙两种产品的年利润分别为y₁万元、y₂万元，直接写出y₁、y₂与x的函数关系式；

（2）分别求出产销两种产品的最大年利润；

（3）为获得最大年利润，该公司应该选择产销哪种产品？请说明理由．