初中数学平行线分线段成比例解答题

已知双曲线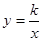的图象经过点A（－1，2）．
（1）求该反比例函数的解析式．
（2）若B（b，m）、C（c，n）是该双曲线上的两个点，且b＜c＜0，判断m，n的大小关系．
（3）判断关于x的一元二次方程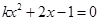的根的情况．

（本题12分）
九年级数学兴趣小组组织了以“等积变形”为主题的课题研究．
第一学习小组发现：如图（1），点A、点B在直线l₁上，点C、点D在直线l₂上，若l₁∥l₂，则S_△ABC=S_△ABD；反之亦成立．

第二学习小组发现：如图（2），点P是反比例函数上任意一点，过点P作x轴、y轴的垂线，垂足为M、N，则矩形OMPN的面积为定值|k|．
请利用上述结论解决下列问题：
（1）如图（3），四边形ABCD、与四边形CEFG都是正方形点E在CD上，正方形ABCD边长为2，则=_________．
（2）如图（4），点P、Q在反比例函数图象上，PQ过点O，过P作y轴的平行线交x轴于点H，过Q作x轴的平行线交PH于点G，若=8，则=_________，k=_________．
（3）如图（5）点P、Q是第一象限的点，且在反比例函数图象上，过点P作x轴垂线，过点Q作y轴垂线，垂足分别是M、N，试判断直线PQ与直线MN的位置关系，并说明理由．

（本题8分）如图，一次函数 y="kx+b" 的图象与反比例函数y=的图象交于 A（﹣2，1），B（1，n）两点．

（1)试确定上述反比例函数和一次函数的表达式；
（2)连OB，在x轴上取点C，使BC=BO，并求△OBC的面积.

（本题共12分）如图，在平面直角坐标系中，正比例函数与反比例函数的图象交于A、B两点，且点A的横坐标为．

（1）求值；
（2）利用图象，直接写出不等式的解集；
（3）过坐标原点O的另一条直线交反比例函数的图象于C、D两点，且C点的纵坐标为2．依次连接AC、CB、BD、DA，求以A、C、B、D为顶点组成的四边形的面积S．

（本题共10分）已知是的反比例函数，且当时，，
求：（1）与之间的函数关系式；
（2）画出这个函数的图像；
（3）试判断点是否在这个函数的图象上。

（本题共8分）如图，一次函数的图象与反比例函数的图象交于A，B两点，

（1）试确定上述反比例函数和一次函数的表达式；
（2）求△AOB的面积。

（本题共8分）已知y=y₁+y₂，其中y₁与x成反比例，y₂与（x-2）成正比例.当x=1时，y=-1；x=3
时，y=3.
（1）求y与x的函数关系式； 
（2）当x=-1时，求y的值。

如图，已知反比例函数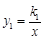（k₁＞0）与一次函数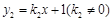相交于A、B两点，AC⊥x轴于点C．若△OAC的面积为1，且tan∠AOC＝2 ．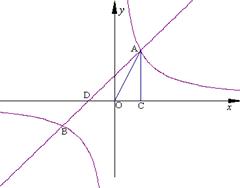

（1）求出反比例函数与一次函数的解析式；
（2）请直接写出B点的坐标，并指出当x为何值时，反比例函数y₁的值大于一次函数y₂的值？

（本题6分）如图，矩形的顶点分别在轴和轴上，点的坐标为．双曲线的图像经过的中点，且与交于点，连接．

（1）求的值及点的坐标；
（2）若点是边OC上一点，且ΔFCB∽ΔDBE，求直线的解析式.

如图，一次函数y＝ax＋b的图象与反比例函数的图象相交于A，B两点，与y轴交于点C，与x轴交于点D，点D的坐标为（－2,0），点A的横坐标是2，tan∠CDO＝.

（1）求点A的坐标；
（2）求一次函数和反比例函数的解析式；
（3）求△AOB的面积．

如图，已知A（4，a）B（-2，-4）是一次函数y=kx+b的图像和反比例函数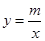的图像的交点．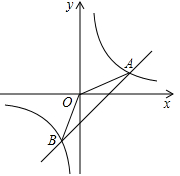

（1）求反比例函数和一次函数的解析式；
（2）根据图象直接写出：当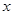取何值时，反比例函数的值大于一次函数的值．
（3）求ΔAOB的面积．

【改编】如图，己知：反比例函数的图象与一次函数y=mx＋b的图象交于点A（1，4），点B（-4，n）．

（1）求一次函数和反比例函数的解析式；
（2）求△OAB的面积．
（3）在直线AB上是否存在点P,使得△AOP是以OP为腰的等腰三角形，若存在，直接写出点P的坐标，若不存在，说明理由．

如图，一次函数与反比例函数的图象交于A（1，m）、B（4，n）两点．

（1）求A、B两点的坐标和反比例函数的解析式；
（2）根据图象，直接写出当y＞y时x的取值范围；
（3）求△AOB的面积．

如图，已知A（－4，），B（-1,2）是一次函数y=kx+b与反比例函数y=（m≠0，m＜0）图象的两个交点，AC⊥x轴于C，BD⊥y轴于D。

（1）根据图象直接回答：在第二象限内，当x取何值时，一次函数大于反比例函数的值?
（2）求一次函数解析式及m的值；
（3）P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P坐标。

一次函数y=ax+b的图象与反比例函数的图象交于A，B两点，与轴交于点C．已知点A（－2，1），点B的坐标为（1，m）．

（1）求反比例函数和一次函数的解析式；
（2）求△AOB的面积。
（3）根据图象写出使一次函数的值小于反比例函数的值的的取值范围．