如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,
tan∠BPD= .延长BD交
.延长BD交 轴于点C,过点D作DA⊥
轴于点C,过点D作DA⊥ 轴,垂足为A,PD与
轴,垂足为A,PD与 轴交于点E,OA=8,OB=6.
轴交于点E,OA=8,OB=6.
(1)求点C的坐标;
(2)若点D在反比例函数y = (k>0)的图象上,求反比例函数的解析式.
(k>0)的图象上,求反比例函数的解析式.
(8分)如图,四边形 是平行四边形,点
是平行四边形,点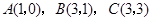 .反比例函数
.反比例函数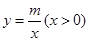 的图象经过点
的图象经过点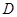 ,点
,点 是一次函数
是一次函数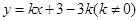 的图象与该反比例函数图象的一个公共点.
的图象与该反比例函数图象的一个公共点.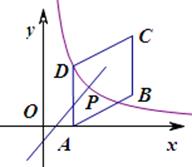
(1)求反比例函数的解析式;
(2)通过计算,说明一次函数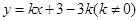 的图象一定过点
的图象一定过点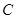 ;
;
(3)对于一次函数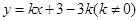 ,当
,当 的增大而增大时,确定点
的增大而增大时,确定点 横坐标的取值范围(不写过程,直接写出结果).
横坐标的取值范围(不写过程,直接写出结果).
如图,在平面直角坐标系中,点A在第一象限,AB⊥x轴,B(2,0),tan∠AOB=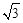 ,过点A的双曲线为
,过点A的双曲线为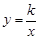 ,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的对应线段O'B'.
,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的对应线段O'B'.
(1)当点O'与点A重合时,求直线l的解析式:
(2)当点B'落在双曲线上时,求出点P的坐标.
如图,反比例函数 (k为常数,且k≠5)经过点A(1,3).
(k为常数,且k≠5)经过点A(1,3).
(1)求反比例函数的解析式;
(2)在x轴正半轴上有一点B,若△AOB的面积为6,求直线AB的解析式.
如图,直线y=﹣x+3与x,y轴分别交于点A,B,与反比例函数的图象交于点P(2,1).
(1)求该反比例函数的关系式;
(2)设PC⊥y轴于点C,点A关于y轴的对称点为A′;
①求△A′BC的周长和sin∠BA′C的值;
②对大于1的常数m,求x轴上的点M的坐标,使得sin∠BMC= .
.
已知反比例函数y= (k≠0)的图象经过点
(k≠0)的图象经过点 (3,2).
(3,2).
(1)求这个函数的解析式;
(2)当-4<x<-1时,求y的取值范围.
如图,一次函数y=kx+b与反比例函数 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.
在平面直角坐标系 中,过点
中,过点 向
向 轴作垂线,垂足为
轴作垂线,垂足为 ,连接
,连接 .双曲线
.双曲线 经过斜边
经过斜边 的中点
的中点 ,与边
,与边 交于点
交于点 .
.
(1)求反比例函数的解析式;
(2)求△ 的面积.
的面积.
某车队要把4000吨货物运到雅安地震灾区(方案定后,每天的运量不变)。
(1)从运输开始,每天运输的货物吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关系式?
(2)因地震,到灾区的道路受阻,实际每天比原计划少运20%,则推迟1天完成任务,求原计划完成任务的天数。
如图,一次函数y=kx+b的图象 与坐标轴分别交于点E、F,与双曲线
与坐标轴分别交于点E、F,与双曲线 交于点P(-1,n),且F是PE的中点.
交于点P(-1,n),且F是PE的中点.
(1)求直线 的解析式;
的解析式;
(2)若直线x=a与 交于点A,与双曲线交于点B(不同于A),问a为何值时,PA=PB?
交于点A,与双曲线交于点B(不同于A),问a为何值时,PA=PB?
(1)如图,过反比例函数 图象上任意一点P(x,y),分别向x轴与y轴作垂线,垂线段分别为PA、PB,证明:
图象上任意一点P(x,y),分别向x轴与y轴作垂线,垂线段分别为PA、PB,证明: ,
, ,
, .
.
(2) 如图,反比例函数 的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,求k的值.
的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,求k的值.
阅读材料:
如图,在平面直角坐标系中,O为坐标原点,对于任意两点A ( ,
, ),
), ,由勾股定理可得:
,由勾股定理可得: ,我们把
,我们把 叫做A、B两点之间的距离,记作
叫做A、B两点之间的距离,记作 .
.
例题:在平面直角坐标系中,O为坐标原点,设点P(x,0).
A(0,2),B (3,-2),则AB= .;PA = .;
解:由定义有 ;
; .
. 表示的几何意义是 .;
表示的几何意义是 .; 表示的几何意义是 ..
表示的几何意义是 ..
解:因为 ,所以
,所以 表示的几何意义是点
表示的几何意义是点 到点
到点 的距
的距
离;同理可得, 表示的几何意义是点
表示的几何意义是点 分别到点(0,1)和点(2,3)的距离和.
分别到点(0,1)和点(2,3)的距离和.
根据以上阅读材料,解决下列问题:
(1)如图,已知直线 与反比例函数
与反比例函数 (
( >0)的图像交于
>0)的图像交于 两点,
两点,
则点A、B的坐标分别为A( , ),B( , ),AB= .
(2)在(1)的条件下,设点 ,则
,则 表示的几何意义
表示的几何意义
是 ;试求 的最小值,以及取得最小值时点P的坐标.
的最小值,以及取得最小值时点P的坐标.
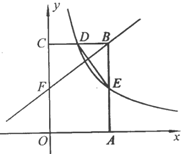
如图,矩形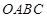 的顶点
的顶点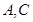 分别在
分别在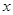 轴和
轴和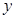 轴上,点
轴上,点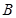 的坐标为
的坐标为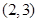 .双曲线
.双曲线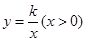 的图像经过
的图像经过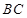 的中点
的中点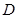 ,且与
,且与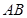 交于点
交于点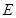 ,连接
,连接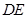 .
.
(1)求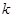 的值及点
的值及点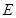 的坐标;
的坐标;
(2)若点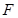 是边上一点,且ΔFCB∽ΔDBE,求直线
是边上一点,且ΔFCB∽ΔDBE,求直线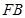 的解析式
的解析式
如图,直线 与
与 轴交于A点,与反比例函数
轴交于A点,与反比例函数 的图象交于点M,过M作MH
的图象交于点M,过M作MH 轴于点H,且tan∠AHO=2.
轴于点H,且tan∠AHO=2.
(1)求k的值,
(2)点N( ,l)是反比例函数
,l)是反比例函数 图象上的点,在
图象上的点,在 轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
如图,一次函数y=kx+b与反比例函数 的图像交于A(m,6),B(3,n)两点。
的图像交于A(m,6),B(3,n)两点。
(1)求一次函数的解析式;
(2)根据图像直接写出 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积。
试题篮
()