初中数学平行线分线段成比例解答题

已知y关于x的反比例函数（m为常数）经过点A（2，-1），求反比例函数的解析式．

如图，反比例函数的图像与一次函数y＝kx＋4的图像相交于P、Q两点，并且P点的纵坐标是6．

（1）求这个一次函数的解析式
（2）求△POQ的面积．

如图，已知A（4，a）B（-2，-4）是一次函数y=kx+b的图像和反比例函数的图像的交点．

（1）求反比例函数和一次函数的解析式；
（2）根据图象直接写出：当取何值时，反比例函数的值大于一次函数的值．
（3）求ΔAOB的面积．

如图，已知：点B（3，3）在双曲线y=（x>0）上，点D在双曲线y=-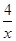（x<0）上，点A和点C分别在x轴，y轴的正半轴上，且点A，B，C，D构成的四边形为正方形．求：
（1）k的值；
（2）点A的坐标.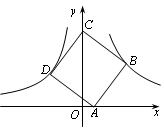

如图，己知：反比例函数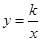的图象与一次函数y=mx＋b的图象交于点A（1，4），点B（-4，n）．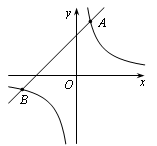

（1）求一次函数和反比例函数的解析式；
（2）求△OAB的面积．

如图，直线y=mx与双曲线y=相交于A，B两点，A点坐标为（1，2）．

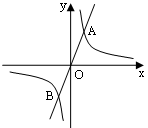
（1）求反比例函数的解析式；
（2）根据函数图像直接写出当mx＞时，x的取值范围；
（3）计算线段AB的长．

如图，直线与反比例函数的图象交于A、B两点，与x轴交于点C，已知点A的坐标为（，m）．

（1）求反比例函数的解析式；
（2）若点P（n，-1）是反比例函数图象上一点，过点P作PE⊥x轴于点E，延长EP交直线AB于点F，求△CEF的面积．

已知抛物线．
（1）求证：无论为任何实数，抛物线与轴总有两个交点；
（2）若A、B是抛物线上的两个不同点，求抛物线的表达式和的值；
（3）若反比例函数的图象与（2）中的抛物线在第一象限内的交点的横坐标为，且满足2<<3，求k的取值范围．

如图，直线y=3x与双曲线的两个交点分别为A （1 ，m）和B．

（1）直接写出点B坐标，并求出双曲线的表达式；
（2）若点P为双曲线上的点（点P不与A、B重合），且满足PO=OB，直接写出点P坐标．

已知反比例函数.
（1）画出该函数的大致图象。
（2）这个函数的大致图象位于哪些象限？函数值y随自变量x的增大如何变化？

已知一次函数y1=ax+b的图象与反比例函数y₂= 的图象相交于A、B两点，坐标分别为(—2，4)、（4，—2）。

（1）求两个函数的解析式；
（2）结合图象写出y₁＜y₂时，x的取值范围；
（3）求△AOB的面积；
（4）是否存在一点P，使以点A﹑B﹑O﹑P为顶点的四边形为菱形？若存在，求出顶点P的坐标；若不存在，请说明理由。

如图，将透明三角形纸片PAB的直角顶点P落在第四象限，顶点A、B分别落在反比例函数y=图象的两支上，且PB⊥x于点C，PA⊥y于点D，AB分别与x轴，y轴相交于点E、F．已知B（1，3）．

（1）k=    ；
（2）试说明AE=BF；
（3）当四边形ABCD的面积为时，求点P的坐标．

如图，一次函数y₁=﹣x+2的图象与反比例函数y₂=的图象相交于A，B两点，与x轴相交于点C．已知tan∠BOC=，点B的坐标为（m，n）．

（1）求反比例函数的解析式；
（2）请直接写出当x＜m时，y₂的取值范围．

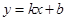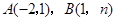如图，一次函数的图象与反比例函数的图象交于两点．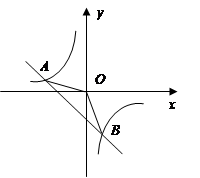

（1）试确定上述反比例函数和一次函数的表达式；
（2）求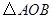的面积．

为了预防“甲流”，某校对教室采用药熏消毒法进行消毒。已知药物燃烧时，室内每立方米空气中的含药量 y（mg）与时间x（min）成正比例，药物燃烧完后，y与x成反比例。现在测得药物8min燃毕，此时室内空气中每立方米含药量6mg，请根据题中所提供信息，解答下列问题：

（1）药物燃烧时，y关于x的函数关系式              ，
药物燃烧后, y关于x的函数关系式              ；
（2）研究表明，每立方米的含药量不超过1．6mg时，学生方可进教室，那么从消毒开始，至少需要经过多少分钟后，学生才能回教室？