初中数学解直角三角形的应用解答题

如图，有一个三角形的钢架 $\mathit{ABC}$， $\angle A=30°$， $\angle C=45°$， $\mathit{AC}=2(\sqrt{3}+1)m$．请计算说明，工人师傅搬运此钢架能否通过一个直径为 $2.1m$的圆形门？

图1是某种路灯的实物图片，图2是该路灯的平面示意图， $\mathit{MN}$ 为立柱的一部分，灯臂 $\mathit{AC}$ ，支架 $\mathit{BC}$ 与立柱 $\mathit{MN}$ 分别交于 $A$ ， $B$ 两点，灯臂 $\mathit{AC}$ 与支架 $\mathit{BC}$ 交于点 $C$ ，已知 $\angle \mathit{MAC}=60°$ ， $\angle \mathit{ACB}=15°$ ， $\mathit{AC}=40\mathit{cm}$ ，求支架 $\mathit{BC}$ 的长．（结果精确到 $1\mathit{cm}$ ，参考数据： $\sqrt{2}\approx 1.414$ ， $\sqrt{3}\approx 1.732$ ， $\sqrt{6}\approx 2.449)$

人字折叠梯完全打开后如图1所示， $B$， $C$是折叠梯的两个着地点， $D$是折叠梯最高级踏板的固定点．图2是它的示意图， $\mathit{AB}=\mathit{AC}$， $\mathit{BD}=140\mathit{cm}$， $\angle \mathit{BAC}=40°$，求点 $D$离地面的高度 $\mathit{DE}$．（结果精确到 $0.1\mathit{cm}$；参考数据 $\sin 70°\approx 0.94$， $\cos 70°\approx 0.34$， $\sin 20°\approx 0.34$， $\cos 20°\approx 0.94)$

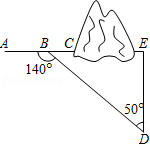
如图，三条笔直公路两两相交，交点分别为、、，测得，，千米，求、两点间的距离．（参考数据：，，结果精确到1千米）．

如图所示，某公路检测中心在一事故多发地段安装了一个测速仪器，检测点设在距离公路 $10m$的 $A$处，测得一辆汽车从 $B$处行驶到 $C$处所用时间为0.9秒，已知 $\angle B=30°$， $\angle C=45°$．

（1）求 $B$， $C$之间的距离；（保留根号）

（2）如果此地限速为 $80\mathit{km}/h$，那么这辆汽车是否超速？请说明理由．（参考数据： $\sqrt{3}\approx 1.7$， $\sqrt{2}\approx 1.4)$

小华同学将笔记本电脑水平放置在桌子上，当显示屏的边缘线 $\mathit{OB}$ 与底板的边缘线 $\mathit{OA}$ 所在水平线的夹角为 $120°$ 时，感觉最舒适（如图① $)$ ．侧面示意图为图②；使用时为了散热，他在底板下面垫入散热架，如图③，点 $B$ 、 $O$ 、 $C$ 在同一直线上， $\mathit{OA}=\mathit{OB}=24\mathit{cm}$ ， $\mathit{BC}\perp \mathit{AC}$ ， $\angle \mathit{OAC}=30°$ ．

（1）求 $\mathit{OC}$ 的长；

（2）如图④，垫入散热架后，要使显示屏的边缘线 $O{B}^{\text{'}}$ 与水平线的夹角仍保持 $120°$ ，求点 $B\text{'}$ 到 $\mathit{AC}$ 的距离．（结果保留根号）

某工程队准备从 $A$到 $B$修建一条隧道，测量员在直线 $\mathit{AB}$的同一侧选定 $C$， $D$两个观测点，如图．测得 $\mathit{AC}$长为 $\frac{3\sqrt{2}}{2}\mathit{km}$， $\mathit{CD}$长为 $\frac{3}{4}(\sqrt{2}+\sqrt{6})\mathit{km}$， $\mathit{BD}$长为 $\frac{3}{2}\mathit{km}$， $\angle \mathit{ACD}=60°$， $\angle \mathit{CDB}=135°(A$、 $B$、 $C$、 $D$在同一水平面内）．

（1）求 $A$、 $D$两点之间的距离；

（2）求隧道 $\mathit{AB}$的长度．

襄阳东站的建成运营标志着我市正式进入高铁时代，郑万高速铁路襄阳至万州段的建设也正在推进中．如图，工程队拟沿 $\mathit{AC}$ 方向开山修路，为加快施工进度，需在小山的另一边点 $E$ 处同时施工．要使 $A$ 、 $C$ 、 $E$ 三点在一条直线上，工程队从 $\mathit{AC}$ 上的一点 $B$ 取 $\angle \mathit{ABD}=140°$ ， $\mathit{BD}=560$ 米， $\angle D=50°$ ．那么点 $E$ 与点 $D$ 间的距离是多少米？

（参考数据： $\sin 50°\approx 0.77$ ， $\cos 50°\approx 0.64$ ， $\tan 50°\approx 1.19)$

问题背景：已知 $\angle \mathit{EDF}$的顶点 $D$在 $\mathit{\Delta ABC}$的边 $\mathit{AB}$所在直线上（不与 $A$， $B$重合）， $\mathit{DE}$交 $\mathit{AC}$所在直线于点 $M$， $\mathit{DF}$交 $\mathit{BC}$所在直线于点 $N$，记 $\mathit{\Delta ADM}$的面积为 $S_1$， $\mathit{\Delta BND}$的面积为 $S_2$．

（1）初步尝试：如图①，当 $\mathit{\Delta ABC}$是等边三角形， $\mathit{AB}=6$， $\angle \mathit{EDF}=\angle A$，且 $\mathit{DE}//\mathit{BC}$， $\mathit{AD}=2$时，则 $S_1·S_2=$　　；

（2）类比探究：在（1）的条件下，先将点 $D$沿 $\mathit{AB}$平移，使 $\mathit{AD}=4$，再将 $\angle \mathit{EDF}$绕点 $D$旋转至如图②所示位置，求 $S_1·S_2$的值；

（3）延伸拓展：当 $\mathit{\Delta ABC}$是等腰三角形时，设 $\angle B=\angle A=\angle \mathit{EDF}=\alpha$．

（Ⅰ）如图③，当点 $D$在线段 $\mathit{AB}$上运动时，设 $\mathit{AD}=a$， $\mathit{BD}=b$，求 $S_1·S_2$的表达式（结果用 $a$， $b$和 $\alpha$的三角函数表示）．

（Ⅱ）如图④，当点 $D$在 $\mathit{BA}$的延长线上运动时，设 $\mathit{AD}=a$， $\mathit{BD}=b$，直接写出 $S_1·S_2$的表达式，不必写出解答过程．

如图，为了测量一栋楼的高度，小明同学先在操场上处放一面镜子，向后退到处，恰好在镜子中看到楼的顶部；再将镜子放到处，然后后退到处，恰好再次在镜子中看到楼的顶部，，，，在同一条直线上），测得，，如果小明眼睛距地面髙度，为，试确定楼的高度．

图①是甘肃省博物馆的镇馆之宝铜奔马，又称“马踏飞燕”，于1969年10月出土于武威市的雷台汉墓，1983年10月被国家旅游局确定为中国旅游标志．在很多旅游城市的广场上都有“马踏飞燕”雕塑．某学习小组把测量本城市广场的“马踏飞燕”雕塑（图②最高点离地面的高度作为一次课题活动，同学们制定了测量方案，并完成了实地测量，测得结果如下表：

课题	测量“马踏飞燕“雕塑最高点离地面的高度
测量示意图				如图，雕塑的最高点到地面的高度为，在测点用仪器测得点的仰角为，前进一段距离到达测点，再用该仪器测得点的仰角为，且点，，，，，均在同一竖直平面内，点，，在同一条直线上．
测量数据	的度数	的度数	的长度		仪器的高度
			5米		1.5米

请你根据上表中的测量数据，帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度（结果保留一位小数）．（参考数据：，，，，，

我国纸伞的制作工艺十分巧妙．如图1，伞不管是张开还是收拢，伞柄 $\mathit{AP}$ 始终平分同一平面内两条伞骨所成的角 $\angle \mathit{BAC}$ ，且 $\mathit{AB}=\mathit{AC}$ ，从而保证伞圈 $D$ 能沿着伞柄滑动．如图2是伞完全收拢时伞骨的示意图，此时伞圈 $D$ 已滑动到点 $D^{\text{'}}$ 的位置，且 $A$ ， $B$ ， $D\text{'}$ 三点共线， $\mathit{AD}\text{'}=40\mathit{cm}$ ， $B$ 为 $\mathit{AD}\text{'}$ 中点．当 $\angle \mathit{BAC}=140°$ 时，伞完全张开．

（1）求 $\mathit{AB}$ 的长．

（2）当伞从完全张开到完全收拢，求伞圈 $D$ 沿着伞柄向下滑动的距离．

（参考数据： $\sin 70°\approx 0.94$ ， $\cos 70°\approx 0.34$ ， $\tan 70°\approx 2.75)$

一座吊桥的钢索立柱 $\mathit{AD}$ 两侧各有若干条斜拉的钢索，大致如图所示．小明和小亮想用测量知识测较长钢索 $\mathit{AB}$ 的长度．他们测得 $\angle \mathit{ABD}$ 为 $30°$ ，由于 $B$ 、 $D$ 两点间的距离不易测得，通过探究和测量，发现 $\angle \mathit{ACD}$ 恰好为 $45°$ ，点 $B$ 与点 $C$ 之间的距离约为 $16m$ ．已知 $B$ 、 $C$ 、 $D$ 共线， $\mathit{AD}\perp \mathit{BD}$ ．求钢索 $\mathit{AB}$ 的长度．（结果保留根号）

如图，为了测量河对岸两点 $A$ ， $B$ 之间的距离，在河岸这边取点 $C$ ， $D$ ．测得 $\mathit{CD}=80m$ ， $\angle \mathit{ACD}=90°$ ， $\angle \mathit{BCD}=45°$ ， $\angle \mathit{ADC}=19°17\text{'}$ ， $\angle \mathit{BDC}=56°19\text{'}$ ．设 $A$ ， $B$ ， $C$ ， $D$ 在同一平面内，求 $A$ ， $B$ 两点之间的距离．

（参考数据： $\tan 19°17\text{'}\approx 0.35$ ， $\tan 56°19\text{'}\approx 1.50$ ． $)$

如图1是一种手机平板支架，由托板、支撑板和底座构成，手机放置在托板上，图2是其侧面结构示意图．量得托板长 $\mathit{AB}=120\mathit{mm}$，支撑板长 $\mathit{CD}=80\mathit{mm}$，底座长 $\mathit{DE}=90\mathit{mm}$．托板 $\mathit{AB}$固定在支撑板顶端点 $C$处，且 $\mathit{CB}=40\mathit{mm}$，托板 $\mathit{AB}$可绕点 $C$转动，支撑板 $\mathit{CD}$可绕点 $D$转动．（结果保留小数点后一位）

（1）若 $\angle \mathit{DCB}=80°$， $\angle \mathit{CDE}=60°$，求点 $A$到直线 $\mathit{DE}$的距离；

（2）为了观看舒适，在（1）的情况下，把 $\mathit{AB}$绕点 $C$逆时针旋转 $10°$后，再将 $\mathit{CD}$绕点 $D$顺时针旋转，使点 $B$落在直线 $\mathit{DE}$上即可，求 $\mathit{CD}$旋转的角度．（参考数据： $\sin 40°\approx 0.643$， $\cos 40°\approx 0.766$， $\tan 40°\approx 0.839$， $\sin 26.6°\approx 0.448$， $\cos 26.6°\approx 0.894$， $\tan 26.6°\approx 0.500$， $\sqrt{3}\approx 1.732)$