初中数学三角形的五心解答题

如图，在△ABC中，AD是BC上的高，AE平分∠BAC，∠B＝75°， ∠C＝45°．求∠DAE与∠AEC的度数．

如图，△ABC中，AB=AC，∠A=40°．

（1）作边AB的垂直平分线MN（保留作图痕迹，不写作法）；
（2）在已作的图中，若MN交AC于点D，连结BD，求∠DBC的度数。

如图，∠BAC=∠DAE，∠ABD=∠ACE，AB=AC．求证：BD=CE．

（1）如图，已知△ABC中，AD⊥BC于D， AE为∠BAC的平分线，∠B=50°，∠C=70°，求∠DAE的度数．

（2）已知在△ABC中，AD⊥BC于点D，AE平分∠BAC（∠C>∠B）．求证：∠DAE=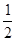（∠C－∠B）．

已知△ABC的三边分别为m²－n²，2mn，m²+n²（m，n为正整数，且m＞n），求证：△ABC是直角三角形．

等腰Rt△ABC中，∠BAC=90°，点A、点B分别是x轴、y轴两个动点，直角边AC交x轴于点D，斜边BC交y轴于点E；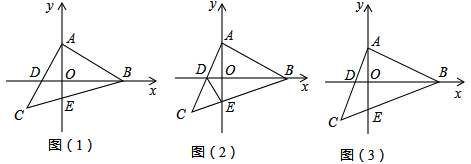

（1）如图（1），若A（0，1），B（2，0），求C点的坐标；
（2）如图（2）， 当等腰Rt△ABC运动到使点D恰为AC中点时，连接DE，求证：∠ADB=∠CDE
（3）如图（3），在等腰Rt△ABC不断运动的过程中，若满足BD始终是∠ABC的平分线，试探究：线段OA、OD、BD三者之间是否存在某一固定的数量关系，并说明理由．

如图，在等腰Rt△ABC中，∠ACB=90^o,AC=CB，F是AB边上的中点,点D、E分别在AC、BC边上运动，且始终保持AD=CE，连接DE、DF、EF．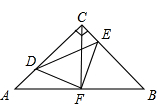

（1）求证：△ADF≌△CEF；
（2）试证明△DFE是等腰直角三角形．

在△ABC中， AB=CB，∠ABC=90°，E为CB延长线上一点，点F在AB上，且AE=CF．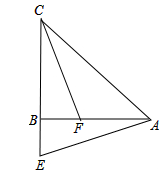

（1）求证：；
（2）若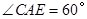，求的度数．

如图，△ABC是等边三角形，BD是中线，延长BC至E，使CE=CD，求证：BD=ED．

如图，∠BAC=∠ABD,AC=BD，点O是AD、BC的交点，点E是AB的中点．试判断OE和AB的位置关系,并给出证明．

如图，∠A=55°，∠B=30°，∠C=35°，求∠BDC的度数．

如图所示，在Rt△ABC中， AB=AC，∠BAC=90°，O为BC中点．如果点M、N分别在线段AB、AC上移动，在移动中保持AN=BM，请判断△OMN的形状，并证明你的结论．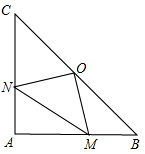

如图，已知点D、E是△ABC的边BC上两点，且BD=CE，∠1=∠2．试证：△ABC是等腰三角形．

如图，⊙O是△的外接圆，，为⊙O的直径，且，连结，求BC的长．

如图，直线l：  交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．

（1）点A坐标是__________，点B的坐标__________，BC=__________．
（2）当点P在什么位置时，△APQ≌△CBP，说明理由．
（3）当△PQB为等腰三角形时，求点P的坐标．