如图,点P是△ABC的边AC上一点,连接BP,以下条件中,不能判定△ABP∽△ACB的是( )
A. |
B. |
| C.∠ABP=∠C | D.∠APB=∠ABC |
如图,点A(3,n)在双曲线 上,过点A作AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点B,则△ABC的周长是( )
上,过点A作AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点B,则△ABC的周长是( )
A.8 B.6 C. D.4
D.4
如图所示,在等边三角形ABC中,O是三个内角平分线的交点,OD∥AB,OE∥AC,则图中等腰三角形的个数是( )
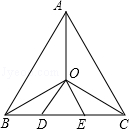
| A.7 | B.6 | C.5 | D.4 |
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人之间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )

| A.②③ | B.①②③ | C.①② | D.①③ |
如图,△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=5cm,BC=3cm,则△PBC的周长等于( )
| A.4cm | B.6cm | C.8cm | D.10cm |
如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( )
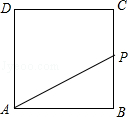
A.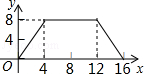 |
B.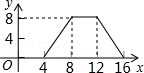 |
C.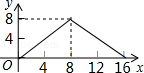 |
D.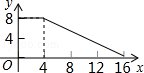 |
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用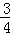 h,立即按原路以另一速度返回,直至与货车相遇.已知货车的速度为60km/h,两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示,现有以下4个结论:
h,立即按原路以另一速度返回,直至与货车相遇.已知货车的速度为60km/h,两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示,现有以下4个结论:

①快递车到达乙地时两车相距120km;
②甲、乙两地之间的距离为300km;
③快递车从甲地到乙地的速度为100km/h;
④图中点B的坐标为(3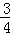 ,75).
,75).
其中,正确的结论有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
平面直角坐标系中,已知A(8,0),△AOP为等腰三角形且面积为16,满足条件的P点有( )
| A.4个 | B.8个 | C.10个 | D.12个 |
已知A、B两地相距900m,甲、乙两人同时从A地出发,以相同速度匀速步行,20min后到达B地,甲随后马上沿原路按原速返回,回到A地后在原地等候乙回来;乙则在B地停留10min后也沿原路以原速返回A地,则甲、乙两人之间的距离s(m)与步行时间t(min)之间的函数关系可以用图象表示为( )
A. B.
B.
C. D.
D.
l00米长的小棒,第1次截去一半,第2次截去剩下的 ,第三次截去剩下的
,第三次截去剩下的 ,如此下去,直到截去剩下的
,如此下去,直到截去剩下的 ,则剩下的小棒长为( )米 。
,则剩下的小棒长为( )米 。
| A.20 | B.15 | C.1 | D.50 |
a为有理数,定义运算符号“※”:当a>-2时,※a=-a;当a<-2时,※a=a;当a=-2时,※a=0.根据这种运算,则※[4+※(2-5)]的值为( )
| A.1 | B.-1 | C.7 | D.-7 |
如图点P按A→B→C→M的顺序在边长为l的正方形边上运动,M是CD边上的中点.设点P经过的路程 为自变量,△APM的面积为
为自变量,△APM的面积为 ,则函数
,则函数 的大致图象是( )
的大致图象是( )
如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是( )
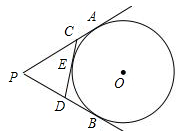
A.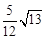 B.
B.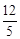 C.
C.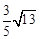 D.
D.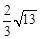
试题篮
()