初中数学解答题

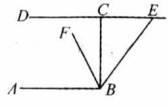
如图， $\mathit{AB}\perp \mathit{BC},\mathit{BC}\perp \mathit{CD}$，在线段 $\mathit{DC}$的延长线上有一个动点 $E$，连接 $\mathit{BE}$，已知 $\mathit{BF}$平分 $\angle \mathit{ABE}$.请问：当点 $E$运动时， $\angle \mathit{BEC}:\angle \mathit{CBF}$的值是否发生变化?如果不发生变化，求出这个比值；如果发生变化，请说明理由.

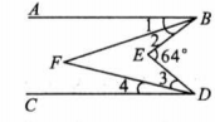
如图所示，一条河流两岸是平行的.当小船行驶到河中 $E$点时，与两岸码头 $B,D$成 ${64}^{\circ }$角；当小船行驶到河中 $F$点时，看 $B$点和 $D$点的视线 $\mathit{FB},\mathit{FD}$恰好有 $\angle 1=\angle 2$， $\angle 3=\angle 4$的关系.你能说出此时点 $F$与码头 $B,D$所形成的角 $\angle \mathit{BFD}$的度数吗?

如图，已知 $\angle A=\angle 1={180}^{\circ }-\angle B,\angle 2={45}^{\circ },\angle 3={75}^{\circ },\mathit{FG}$平分 $\angle \mathit{DFE}$.求 $\angle \mathit{CFG}$的度数.

如图， $\mathit{CD}//\mathit{EF},\angle 1+\angle 2=\angle \mathit{ABC}$，求证： $\mathit{AB}//\mathit{GF}$.

两条直线相交，四个交角中的一个锐角（或一个直角）称为这两条直线的“夹角”（如图），如果在平面上画 $L$条直线，要求它们两两相交，并且“夹角”只能是 $15°，30°，45°，60°，75°，90°$其中之一，问：

（1） $L$的最大值是什么?

（2）当 $L$取最大值时，问所有的“夹角”的和是多少?

在一个平面上有 $2017$条直线，最多能将这一平面分成多少个部分.

平面上有 $10$条直线，无任何三条交于一点，欲使它们出现 $31$个交点，怎样安排才能办到?（只要求画出符合条件的 $10$条直线）

能否在平面上画出 $7$条直线（任意 $3$条都不共点），使得它们中的每条直线都恰好与另 $3$条直线相交?如果能，请画出一例，如果不能，请简述理由.

平面上 $7$条直线两两相交，试证明：在所有的交角中，至少有一个角小于 $26°$.

在直角坐标系中，有以 $A\left(-1\mathrm{，}-1\right)，B\left(1\mathrm{，}-1\right)，C\left(1\mathrm{，}1\right)，D\left(-1\mathrm{，}1\right)$为顶点的正方形，设它在折线 $y=|x-a|+a$上侧部分的面积为 $S$，求 $S$关于 $a$的函数关系式.

编号为 $1$到 $25$的 $25$个弹珠被分别放在两个篮子 $A$和 $B$中， $15$号弹珠在篮子 $A$中，把这个弹珠从篮子 $A$移至篮子 $B$中，这时篮子 $A$中的弹珠号码数的平均数等于原平均数加 $\frac{1}{4}\mathrm{，}B$篮中弹珠号码数的平均数也等于原平均数加 $\frac{1}{4}$，问原来在篮子 $A$中有多少个弹珠?

我国是水资源比较贫乏的国家之一，各地采用了价格调控等手段来达到节约用水的目的.某市用水收费的方法是：水费 $=$基本费十超额费十定额损耗费.若每月用水量不超过最低限量 $a{\mathrm{m}}^3$时，只付基本费 $8$元和每月的定额损耗费 $c$元；若用水量超过 $a{\mathrm{m}}^3$时，除了付同上的基本费和定额损耗费外，超过部分每立方米付 $b$元的超额费.已知每户每月的定额损耗费不超过 $5$元.

（1）当月用水量为 $x{\mathrm{m}}^3$时，支付费用为 $y$元，写出 $y$关于 $x$的函数关系式；

（2）该市一家庭今年一季度的用水量和支付费用见下表，根据表中数据求 $a\mathrm{，}b\mathrm{，}c$.

如图，在四边形 $\mathit{ABCD}$中， $\mathit{AD}//\mathit{BC}\mathrm{，}\angle B={90}^{\circ }\mathrm{，}\mathit{AB}=6\sqrt{3}\mathrm{cm}\mathrm{，}\mathit{AD}=18\mathrm{cm}\mathrm{，}\mathit{BC}=24\mathrm{cm}$.点 $P$从点 $A$出发，以 $1\mathrm{cm}/\mathrm{s}$的速度向 $D$点运动；点 $Q$从点 $C$同时出发，以 $3\mathrm{cm}/\mathrm{s}$的速度向点 $B$运动，规定其中一个动点到达端点时，另一个动点也随之停止运动.设运动时间为 $t\left(s\right)$.

（1） $t$为何值时，四边形 $\mathit{ABQP}$是矩形?

（2） $t$为何值时，四边形 $\mathit{PQCD}$是平行四边形?

（3）在其它条件不变的情况下，能否通过改变点 $Q$的运动速度，使得四边形 $\mathit{PQCD}$是菱形?

设 $x=\frac{\sqrt{n+1}-\sqrt{n}}{\sqrt{n+1}+\sqrt{n}}\mathrm{，}y=\frac{\sqrt{n+1}+\sqrt{n}}{\sqrt{n+1}-\sqrt{n}}\mathrm{，}n$为自然数，如果 $2x^2+197\mathit{xy}+2y^2=1993$成立，求 $n$的值.

为增强公民的节约意识，合理利用天然气资源，某市自1月1日起对市区民用管道天然气价格进行调整，实行阶梯式气价，调整后的收费价格如表所示：

（1）若甲用户 $3$月份的用气量为 $60m^3$，则应缴费＿＿＿＿＿元；

（2）若调价后每月支出的燃气费为 $y$（元），每月的用气量为 $x$（ $m^3$）， $y$与 $x$之间的关系如下图所示，求 $a$的值及 $y$与 $x$之间的函数关系式；

（3）在（2）的条件下，若乙用户 $2，3$月份共用气 $175m^3$（ $3$月份用气量低于 $2$月份用气量），共缴费 $455$元，乙用户 $2，3$月份的用气量各是多少？