“五・一”假期,某火车客运站旅客流量不断增大,旅客往往需要长时间排队等候检查.经调查发现,在车站开始检票时,有 人排队检票.检票开始后,仍有旅客继续前来排队检票进站.设旅客按固定的速度增加,检票口检票的速度也是固定的.检票时,每分钟候车室新增排队检票进站 人,每分钟每个检票口检票 人.已知检票的前 只开放了两个检票口.某一天候车室排队等候检票的人数 (人)与检票时间 (分钟)的关系如图所示.
(1)求 的值;
(2)求检票到第 时,候车室排队等候检票的旅客人数;
(3)若要在开始检票后 内让所有排队的旅客都能检票进站,以便后来到站的旅客随到随检,问检票一开始至少需要同时开放几个检票口?

在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成的长方形的周长与面积相等,则这个点叫做和谐点.例如在图中,过点 分别作 轴, 轴的垂线,与坐标轴围成的长方形 的周长与面积相等,则点 是和谐点.
(1)判断点 是否为和谐点,并说明理由;
(2)若和谐点 在直线 ( 为常数)上,求 的值.

小华观察钟面(图(1)),了解到钟面上的分针每小时旋转 度,时针每小时旋转 度.他为了进一步研究钟面上分针与时针的旋转规律,从下午 开始对钟面进行了一个小时的观察,为了方便,他将分针与时针原始位置 (图(2))的夹角记为 度,时针与原始位置 的夹角记为 度,(夹角是指不大于平角的角),旋转时间为 ,观察结束后,他利用所得的数据制成图象(图(3)),并求出 与 的函数关系式
请你完成:
(1)求出题图(3)中 与 的函数关系式;
(2)直接写出 两点的坐标,并解释这两点的实际意义;
(3)若小华继续观察一小时,请你在图(3)中补全图象.

市, 市和 市分别有某种机器 台, 台和 台。现决定把这些机器支援给 市 台, 市 台。已知从 市调运一台机器到 市, 市的运费分别为 元和 元;从 市调运一台机器到 市, 市的运费分别为 元和 元;从 市调运一台机器到 市, 市的运费分别为 元和 元.
(1)设从 市, 市各调运 台机器到 市,当 台机器全部调运完毕后,求总运费 (元)关于 (台)的函数式,并求 的最小值和最大值;
(2)设从 市调 台到 市, 市调 台到 市,当 台机器全部调运完毕后,用 表示总运费 (元),并求 的最小值和最大值.
某商业集团新进了 台空调, 台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中 台给甲连锁店, 台给乙连锁店.两个连锁店销售这两种电器每台的利润(元)如下表:

设集团调配给甲连锁店 台空调,集团卖出这 台电器的总利润为 (元)。
(1)写出 关于 的函数解析式,并求出 的取值范围;
(2)为了促销,集团决定仅对甲连锁店的空调每台让利 元销售,其他的销售利润不变,并且让利后每台空调的利润仍然高于甲连锁店销售的每台冰箱的利润,问该集团应该如何设计调配方案,使总利润达到最大?
有一个附有进、出水管的容器,每单位时间内进、出的水量都是一定的,设从某时开始 钟内只进水不出水,在随后的 内既进水又出水,得到时间 与水量 之间的关系如图所示,若 后只出水不进水,求这时(即 ) 与 之间的函数关系式,并求出多长时间可将容器内的水放完?
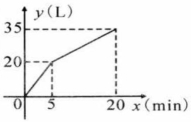
如图,表示甲、乙两名选手在一次自行车越野赛中,路程 随时间 变化的图象(全程).根据图象回答下列问题:
(1)比赛开始多少分钟时,两人第一次相遇?
(2)这次比赛全程是多少千米?
(3)比赛开始多少分钟时,两人第二次相遇?
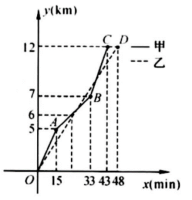
如图所示。设函数 的图象与 轴交于 点,函数 的图象与 轴交于点 ,两个函数的图象交于点 ,求通过线段 的中点 及 点的一次函数解析式.

在 两个数之间,第一次写上 ,第二次在 之间和 之间分别写上 和 ,如下所示:
第 次操作:
第 次操作:
第 次操作:
第 次操作:…
第 次操作是在上一次操作的基础上,在每两个相邻的数之间写上这两个数的和的 .
(1)请写出第 次操作后所得到的 个数,并求出它们的和;
(2)经过 次操作后所有数的和记为 ,第 次操作后所有数的和记为 ,写出 与 之间的关系式;
(3)求 的值.
点 分别在一次函数 与 的图象上,其横坐标分别为 ,若直线 为一次函数 的图象,当 是整数时,求满足条件的整数 的值.
如图,已知直线 与 轴, 轴分别交于点 和点 ,另一直线 经过 ,且把 分成两部分.
(1)若 被分成的两部分面积相等,求 和 的值;
(2)若 被分成的刑部分的面积比为 ,求 和 的值.
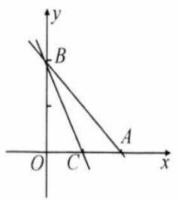
某造纸厂有甲和乙两个长方体蓄水池,将甲蓄水池中的水以每小时 的速度注人乙蓄水池.甲、乙两个蓄水池中水的深度 与注水时间 的函数关系如图所示.结合图象回答下列问题:
(1)分别求出甲蓄水池和乙蓄水池中水的深度 与注水时间 之间的函数关系式(不必写出 的取值范围);
(2)求注水多长时间甲蓄水池和乙蓄水池中水的深度相同;
(3)求注水多长时间甲、乙两个蓄水池的蓄水量相同.
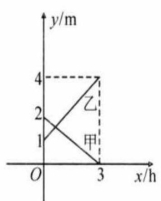
如图,直线 的解析式为: ,且 与 轴交于点 ,直线 经过点 ,直线 交于点 .
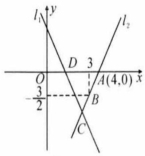
(1)求点 的坐标;
(2)求直线 的解析式;
(3)求 的面积;
(4)在直线 上存在异于点 的另一点 ,使得 与 的面积相等,请直接写出点 的坐标.
试题篮
()