高中数学合情推理和演绎推理试题

有一个数阵如下：记第行的第个数字为，（如），则等于        .

设向量 $a_k=(\cos \frac{k\pi }{6},\sin \frac{k\pi }{6}+\cos \frac{k\pi }{6})(k=0,1,2,...,12)$，则 $\underset{k=0}{\overset{11}{\sum }}(a_k·a_{k+1})$的值为.

古希腊毕达哥拉斯学派的数学家研究过各种多边形数.如三角形数，第个三角形数为.记第个边形数为（），以下列出了部分边形数中第个数的表达式：
三角形数             正方形数  
五边形数             六边形数  
可以推测的表达式，由此计算            .

已知x∈R_＋，有不等式：x＋≥2＝2，x＋＝＋＋≥3＝3，…．启发我们可能推广结论为：x＋≥n＋1（n∈N^*），则a的值为 （ ）

A．2^n

B．n^n

C．n^2

D．2^n^＋1

观察下列等式:,…,根据上述规律,第五个等式为______________．

平面几何中，有边长为的正三角形内任一点到三边距离之和为定值，类比上述命题，棱长为 的正四面体内任一点到四个面的距离之和为             （   ）

A．

B．

C．

D．

如图所示的三角形数阵叫“莱布尼兹调和三角形”，它们是由整数的倒数组成的，第行有个数且两端的数均为，每个数是它下一行左右相邻两数的和，如， ，，…，则第7行第4个数(从左往右数)为(  )

A．

B．

C．

D．

某种平面分形图如下图所示，一级分形图是由一点出发的三条线段，长度均为1，两两夹角为； 二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来的线段,且这两条线段与原线段两两夹角为；……；依此规律得到级分形图．

（1）4级分形图中共有______条线段；
（2）级分形图中所有线段长度之和为      ．

如图所示的三角形数阵叫“牛顿调和三角形”，它们是由整数的倒数组成的，第n行有n个数且两端的数均为，每个数是它下一行左右相邻两数的和，如 
，…，

则（1）第6行第2个数（从左往右数）为_________；
（2）第n行第3个数（从左往右数）为_________．

已知，由不等式我们可以得出推广结论：，则（ ）   

A．

B．

C．

D．

设函数f (x)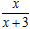＝ (x＞0)，观察：f ₁(x)＝f (x)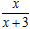＝， f ₂(x)＝f (f ₁(x))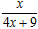＝，f ₃(x)＝f (f ₂(x))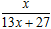＝，f ₄(x)＝f (f ₃(x))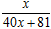＝……，根据以上事实，由归纳推理可得：当n∈N^*，n≥2时，f_n(x)＝f (f_n－1(x))＝           .

如下图所示将若干个点摆成三角形图案，每条边（包括两个端点）有n（n>l，n∈N^*）个点，相应
的图案中总的点数记为，则=（  ）

A．

B．

C．

D．

的所有正约数之和可按如下方法得到：因为，所以的所有正约数之和为，参照上述方法，可求得的所有正约数之和为          ．

计算，可以采用以下方法：
构造等式：，两边对x求导，
得，
在上式中令，得．类比上述计算方法，计算            ．

根据下面一组等式：
S₁＝1；
S₂＝2＋3＝5；
S₃＝4＋5＋6＝15；
S₄＝7＋8＋9＋10＝34；
S₅＝11＋12＋13＋14＋15＝65；
S₆＝16＋17＋18＋19＋20＋21＝111；
S₇＝22＋23＋24＋25＋26＋27＋28＝175；
……
可得________．