如图,四边形PCBM是直角梯形, ,
, ,
, ,
, .又
.又 ,
, ,
, ,直线
,直线 与直线
与直线 所成的角为60°.
所成的角为60°.
(1)求证: ;
;
(2)求三棱锥 的体积.
的体积.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1。
(1)请在线段CE上找到一点F,使得直线BF∥平面ACD,并证明;
(2)求平面BCE与平面ACD所成锐二面角的大小;
[2012·辽宁高考]已知正三棱锥P-ABC,点P,A,B,C都在半径为 的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.
的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.
如图,在中,
,
,
是
上的高,沿
把是
上的
折起,使
.
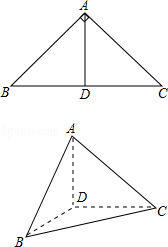
(Ⅰ)证明:平面平面
;
(Ⅱ)设,求三棱锥
的表面积.
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形,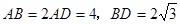
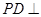 底面
底面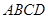
(1)证明:平面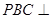 平面
平面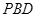 ;
;
(2)若二面角 大小为
大小为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.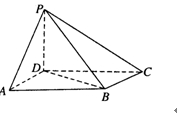
已知正△ABC的边长为 , CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
, CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
(1)试判断折叠后直线AB与平面DEF的位置关系,并说明理由;
(2)若棱锥E-DFC的体积为 ,求
,求 的值;
的值;
(3)在线段AC上是否存在一点P,使BP⊥DF?如果存在,求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
如图,四棱锥P-ABCD中,底面ABCD为正方形,DA⊥面ABP,AB=1,PA=2,∠PAB=600,E为PA的中点,F为PC上不同于P、C的任意一点.
(1)求证:PC∥面EBD
(2)求异面直线AC与PB间的距离
(3)求三棱锥E-BDF的体积.
如图, ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, ,
, 分别是
分别是 ,
, 的中点,
的中点, .
.
(1)证明: ;
;
(2)证明: ;
;
(3)假设这是个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果鱼游到四棱锥 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.
如图,四棱锥 中,
中, ⊥底面
⊥底面 ,底面
,底面 为菱形,点
为菱形,点 为侧棱
为侧棱 上一点.
上一点.
(1)若 ,求证:
,求证: 平面
平面 ;
;
(2)若 ,求证:平面
,求证:平面 ⊥平面
⊥平面 .
.
如图,在四棱柱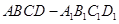 中,底面ABCD和侧面
中,底面ABCD和侧面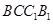 都是矩形,E是CD的中点,
都是矩形,E是CD的中点, ,
, .
.
(1)求证: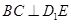 ;
;
(2)若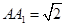 ,求三棱锥
,求三棱锥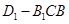 的体积.
的体积.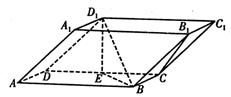
已知三条不重合的直线 和两个不重合的平面
和两个不重合的平面 ,下列命题正确的是( )
,下列命题正确的是( )
A.若 , , ,则 ,则 |
B.若 , , ,且 ,且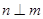 ,则 ,则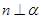 |
C.若 , ,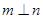 ,则 ,则 |
D.若 , , ,且 ,且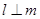 ,则 ,则 |
试题篮
()