高中数学空间向量的应用试题

如图所示， 四棱锥P－ABCD的底面是边长为1的正方形，PA^CD，PA = 1，PD＝，E为PD上一点，PE = 2ED．
（1）求证：PA ^平面ABCD；
（2）求二面角D－AC－E的余弦值；
（3）在侧棱PC上是否存在一点F，使得BF // 平面AEC？
若存在，指出F点的位置，并证明；若不存在，说明理由．

如图，四棱锥中，底面是平行四边形，，平面，，，是的中点.
（1）求证：平面；
（2）求平面与平面所成锐二面角的余弦值.

已知m、n为两条不同的直线，、为两个不同的平面，下列命题中正确的是 （ ） 

A．若∥，m∥，则m∥	B．若m⊥，m⊥，则∥
C．若⊥，m⊥，则m⊥	D．若m∥，m⊥n，则n⊥

如图,在四棱柱中,已知平面平面且,.
(1) 求证:
(2) 若为棱上的一点,且平面,求线段的长度

如图，已知四棱锥P-ABCD的底面为直角梯形，AD∥BC，∠BCD=90⁰，
PA=PB，PC=PD．
（1）试判断直线CD与平面PAD是否垂直，并简述理由；
（2）求证：平面PAB⊥平面ABCD；
（3）如果CD=AD+BC，二面角P-CB-A等于60⁰，求二面角P-CD-A的大小．

已知三棱锥中，，，，，分别是，中点．

（1）求证：；
（2）求直线与平面所成角的正弦值．

如图，三棱柱中，侧面为菱形，的中点为，且平面.

（1）证明：

（2）若,求三棱柱的高.

在如图所示的多面体中，四边形和都为矩形。

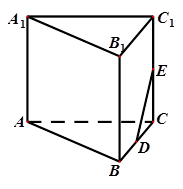
（Ⅰ）若，证明：直线平面；
（Ⅱ）设分别是线段的中点，在线段AB上是否存在一点，使直线平面？请证明你的结论。

如图1，四边形 $ABCD$为矩形， $PD\perp$平面 $ABCD$， $AB=1,BC=PC=2$，作如图2折叠，折痕 $EF//DC$.其中点 $E,F$分别在线段 $PD,PC$上，沿 $EF$折叠后点 $P$在线段 $AD$上的点记为 $M$，并且 $MF\perp CF$.

（1）证明： $CF\perp$平面 $MDF$；
（2）求三棱锥 $M-CDE$的体积.

若空间中四条直线两两不同的直线，满足，则下列结论一定正确的是（   ）

A．		B．
C．	既不平行也不垂直	D．	的位置关系不确定

如图，三棱锥中，,.

（1）求证：；
（2）若，为中点，求三棱锥的体积.

如图在三棱锥 $P-ABC$中， $D,E,F$分别为棱 $PC,AC,AB$的中点，已知 $PA\perp AC,PA=6,BC=8,DF=5$.

求证：

（1）直线 $PA//$平面 $DEF$；
（2）平面 $BDE$ $\perp$平面 $ABC$.

如图，三棱柱中，侧面为菱形，.

（Ⅰ）证明：;
（Ⅱ）若，,,求二面角的余弦值.

如图,在四棱柱 $ABCD-A_1{B}_1{C}_1{D}_1$中,底面 $ABCD$是等腰梯形, $\angle DAB={60}^{°},AB=2CD=2,M$是线段 $AB$的中点.

（Ⅰ）求证: $C_{1}M\parallel A_{1}AD{D}_1$；
（Ⅱ）若 $C{D}_1$垂直于平面 $ABCD$且 $C{D}_1=\sqrt{3}$,求平面 $C_1{D}_{1}M$和平面 $ABCD$所成的角(锐角)的余弦值.

如图，四棱锥中，为矩形，平面平面.

(1)求证：

(2)若问为何值时，四棱锥的体积最大？并求此时平面与平面夹角的余弦值.