如图所示几何体是正方体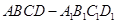 截去三棱锥
截去三棱锥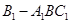 后所得,点
后所得,点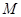 为
为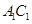 的中点.
的中点.
(1) 求证: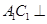 平面
平面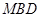 ;
;
(2) 当正方体棱长等于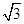 时,求三棱锥
时,求三棱锥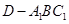 的体积.
的体积.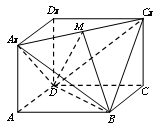
如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证:
(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.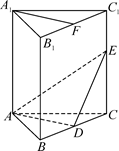
设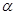 为平面,a、b为两条不同的直线,则下列叙述正确的是( )
为平面,a、b为两条不同的直线,则下列叙述正确的是( )
A.若a∥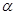 ,b∥ ,b∥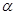 ,则a∥b ,则a∥b |
B.若a⊥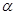 ,a∥b,则b⊥ ,a∥b,则b⊥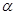 |
C.若a⊥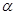 ,a⊥b,则b∥ ,a⊥b,则b∥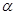 |
D.若a∥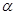 ,a⊥b,则b⊥ ,a⊥b,则b⊥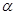 |
如图,已知三角形△ABC与△BCD所在平面相互垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.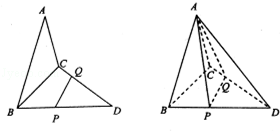
(Ⅰ)求证:AB⊥CQ;
(Ⅱ)求BP的长;
(Ⅲ)求直线AP与平面BCD所成的角.
已知两条不同的直线m、n,两个不同的平面a、β,则下列命题中的真命题是( )
| A.若m⊥a,n⊥β,a⊥β,则m⊥n |
| B.若m⊥a,n∥β,a⊥β,则m⊥n |
| C.若m∥a,n∥β,a∥β,则m∥n |
| D.若m∥a,n⊥β,a⊥β,则m∥n |
如图所示的几何体中,四边形ABCD是等腰梯形,AB//CD,  ,FC
,FC  平面ABCD, AE
平面ABCD, AE  BD,CB =CD=-CF.
BD,CB =CD=-CF.
(Ⅰ)求证:平面ABCD  平面AED;
平面AED;
(Ⅱ)直线AF与面BDF所成角的余弦值
已知直线 ,平面
,平面 ,且
,且 ,下列命题中正确命题的个数是
,下列命题中正确命题的个数是
①若 ,则
,则  ②若
②若 ,则
,则
③若 ,则
,则 ; ④若
; ④若 ,则
,则
A.1 B.2 C.3 D.4
试题篮
()