如图,四边形为正方形,
平面
,
,
于点
,
,交
于点
.

(1)证明:平面
;
(2)求二面角的余弦值.
在平行四边形
中,
,
.将
沿
折起,使得平面
平面
,如图.

(1)求证:
;
(2)若
为
中点,求直线
与平面
所成角的正弦值.
如图,四棱锥中,底面是以
为中心的菱形,
底面
,
,
为
上一点,且
.
(1)证明:平面
;
(2)若,求四棱锥
的体积.

如图,在四棱锥
中,平面
平面
;
,
.
(1)证明:
平面
;
(2)求直线
与平面
所成的角的正切值.

下列命题:①已知平面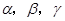 满足
满足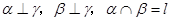 则
则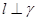 .
.
②E,F,G,H是空间四边形ABCD各边AB,BC,CD,DA的中点,若对角线BD=2,AC=4,则
③过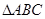 所在平面
所在平面 外一点P,作
外一点P,作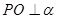 ,垂足为O,连接PA,PB,PC,若
,垂足为O,连接PA,PB,PC,若 ,则点O是
,则点O是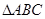 的垂心
的垂心
其中正确命题的序号是 。
如图,在长方体 中,
中, .
.
(1)若点 在对角线
在对角线 上移动,求证:
上移动,求证: ⊥
⊥ ;
;
(2)当 为棱
为棱 中点时,求点
中点时,求点 到平面
到平面 的距离。
的距离。 
在 类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为________________.
类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为________________.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(1)求证:AB1⊥面A1BD;
(2)求二面角A-A1D-B的余弦值;
(3)求点C到平面A1BD的距离.
在 类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为__________________________.
类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为__________________________.
如图, ,
, 为圆柱
为圆柱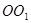 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径,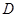 ,
, 分别是
分别是 ,
, 的中点,
的中点,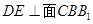 .
.
(1)证明: ;
;
(2)证明: ;
;
(3)假设这是个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果鱼游到四棱锥 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4, ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点.
(1)求证:平面AHC 平面
平面 ;(2)(2)求此几何体的体积.
;(2)(2)求此几何体的体积.
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4, ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点.
(1)求证:平面AHC 平面
平面 ;(2)点M在直线EF上,且
;(2)点M在直线EF上,且 平面
平面 ,求平面ACH与平面ACM所成锐角的余弦值.
,求平面ACH与平面ACM所成锐角的余弦值.
如图,已知 平面
平面 ,
, ,
, ,
,
且 是
是 的中点,
的中点, .
.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求此多面体的体积.
如图,在四棱锥 中,底面
中,底面 是边长为
是边长为 的正方形,侧面
的正方形,侧面

底面 ,且
,且 ,
, 、
、 分别为
分别为 、
、 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:面
 平面
平面 ;
;
(3)在线段 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?说明理由.
?说明理由.
试题篮
()